Предмет: Математика,
автор: Аноним
Определённый интеграл
Помогите пожалуйста решить задачки, с показом всех шагов!
Приложения:
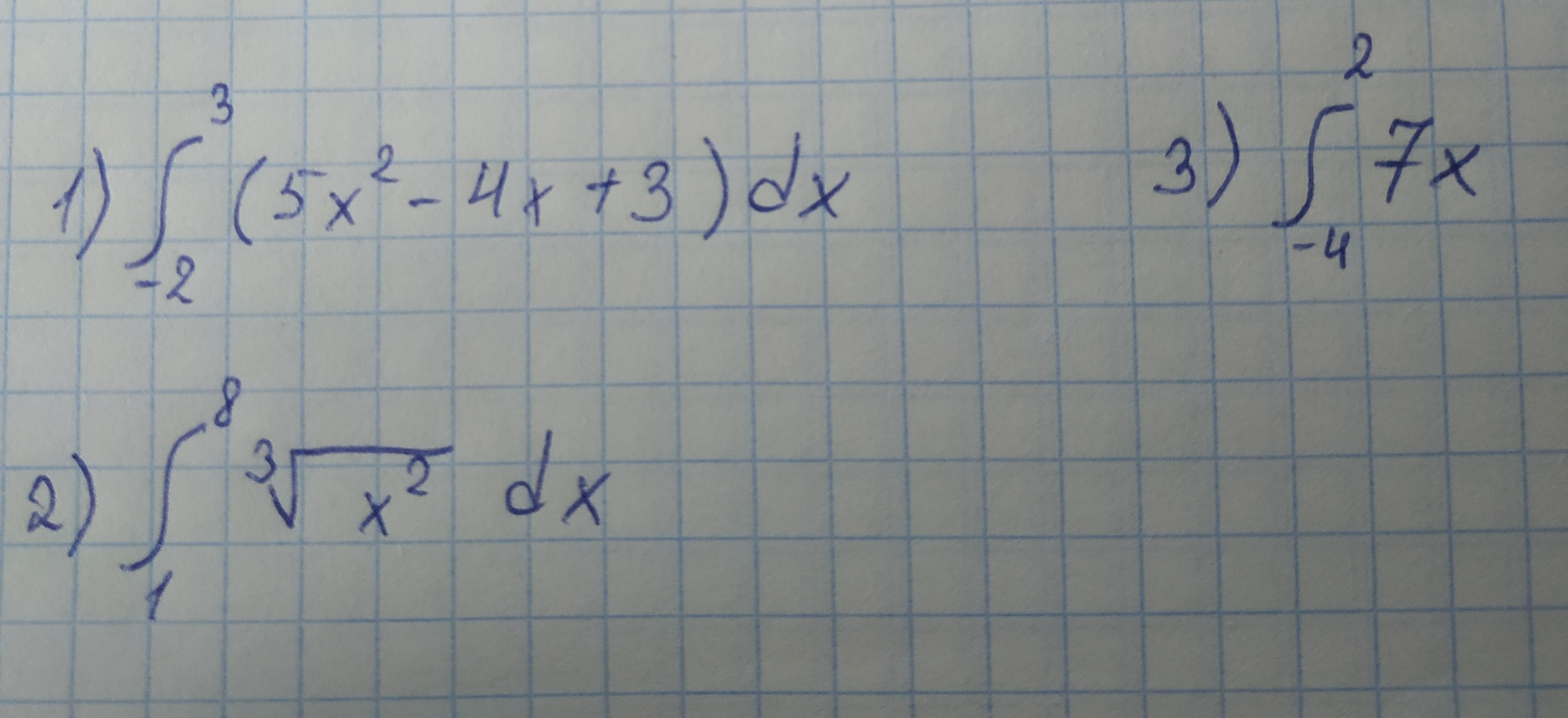
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1)
2)
3)
Похожие вопросы
Предмет: Українська мова,
автор: alexsakeig
Предмет: Русский язык,
автор: Nurmagomedova20
Предмет: Русский язык,
автор: mssvinuhova
Предмет: Русский язык,
автор: sss131
Предмет: Математика,
автор: bogdanr2404