Question

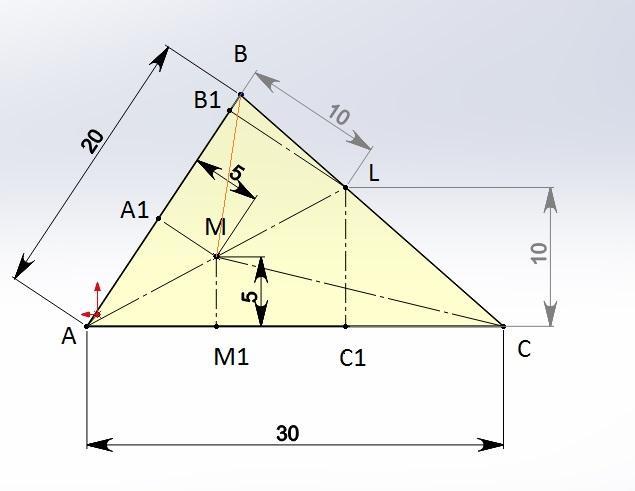
Точка M — середина биссектрисы AL треугольника ABC. Известно, что AB=20, AC=30, а площадь треугольника ABM равна 50. Найдите площадь треугольника MLC.


​

Answer 1

Ответ:

S ΔМLC=75

Объяснение:

Высота А₁М ΔАВМ определяется из S Δ АВМ=50

S Δ АВМ=0,5*АВ*А₁М  А₁М =2*S Δ АВМ/АВ=2*50/20=5

Найдем площадь ΔМLС

S ΔМLC=S Δ АСL-S Δ АМС=150-0,5*5*30=75

S Δ АCL=0,5*AC*C₁L=0,5*30*10=150

Любая точка на биссектрисе ∠А равноудалена от сторон АВ и АС

А₁М=М₁М=5

Из подобия  Δ АММ₁ и Δ АLС с коэффициентом подобия 2

С₁L=2М₁М=10