Предмет: Алгебра,
автор: prissofia2803
Обчислити інтеграл / вычислить интеграл
Приложения:
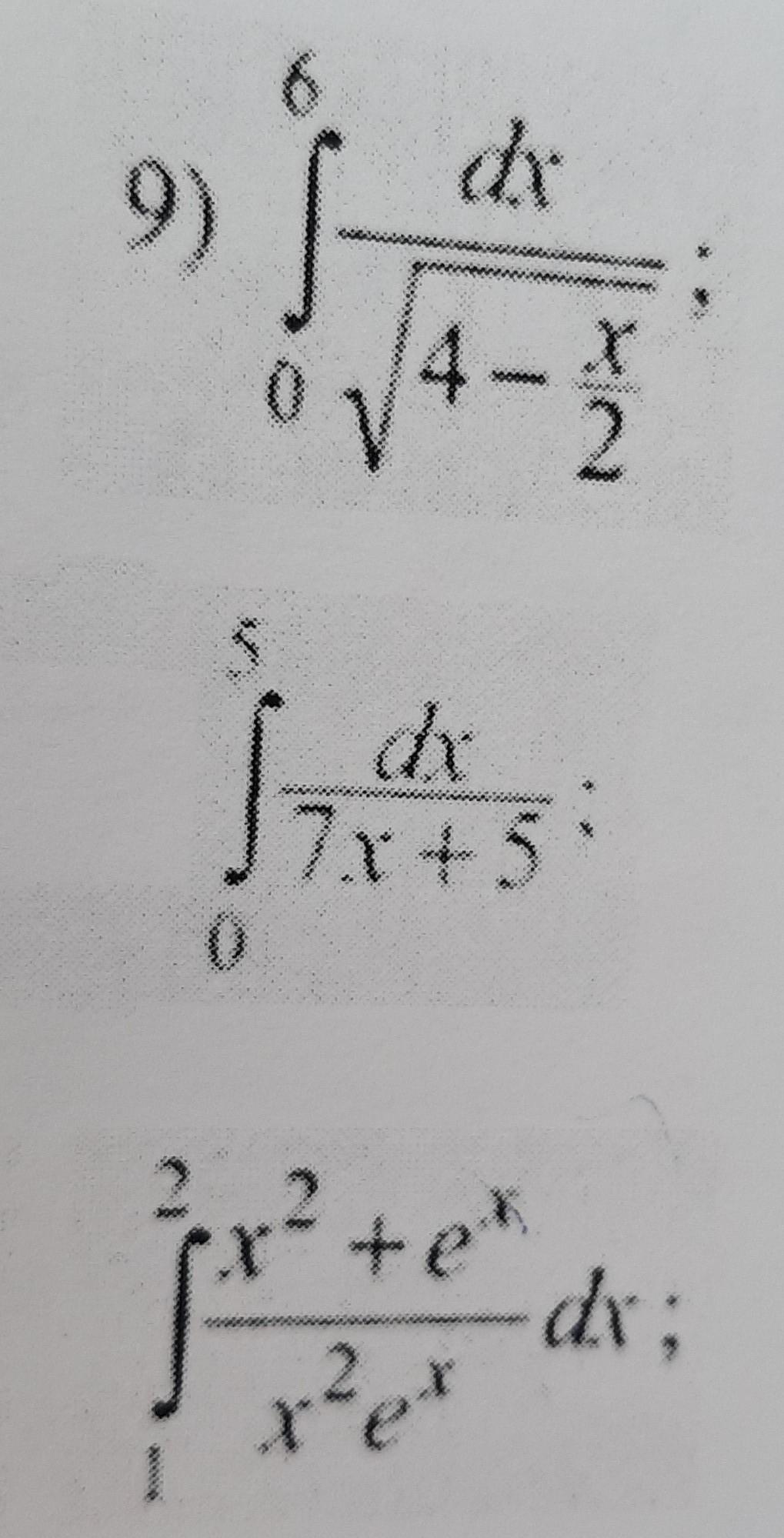
Ответы
Автор ответа:
2
Ответ:
NNNLLL54:
Смотря как учить ... Интенсивно, каждый день, обязательно с решением большого количества примеров самостоятельно.
Вам там уже всё правильно решили. А задач надо решать побольше. Зайди на канал к какому-нибудь преподу. и послушай, как объясняют решение геометрических задач. Не забывай отдыхать, на воздухе, иначе твои старания пропадут даром .
Автор ответа:
1
Відповідь: фото
Пояснення:
Приложения:
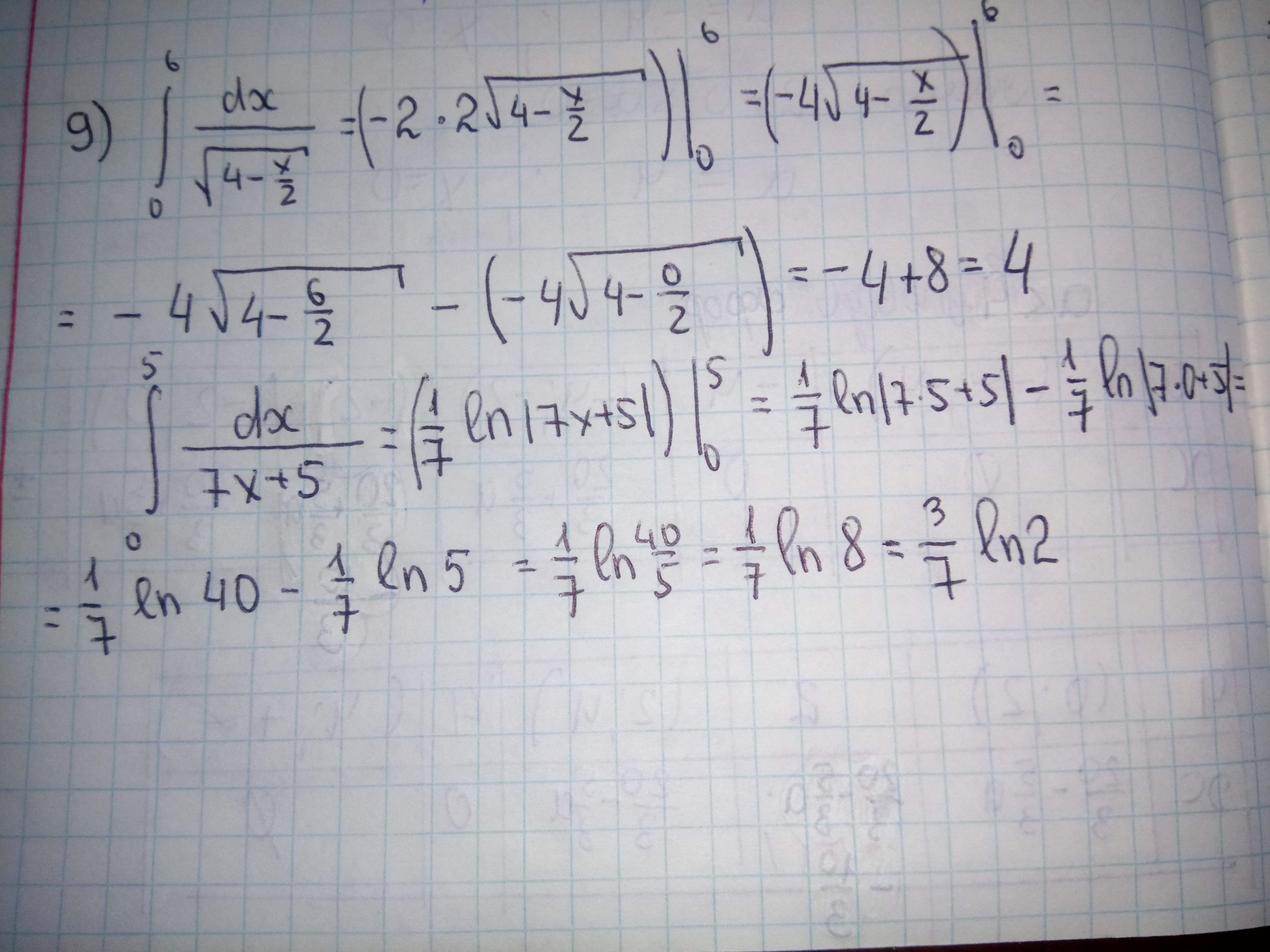
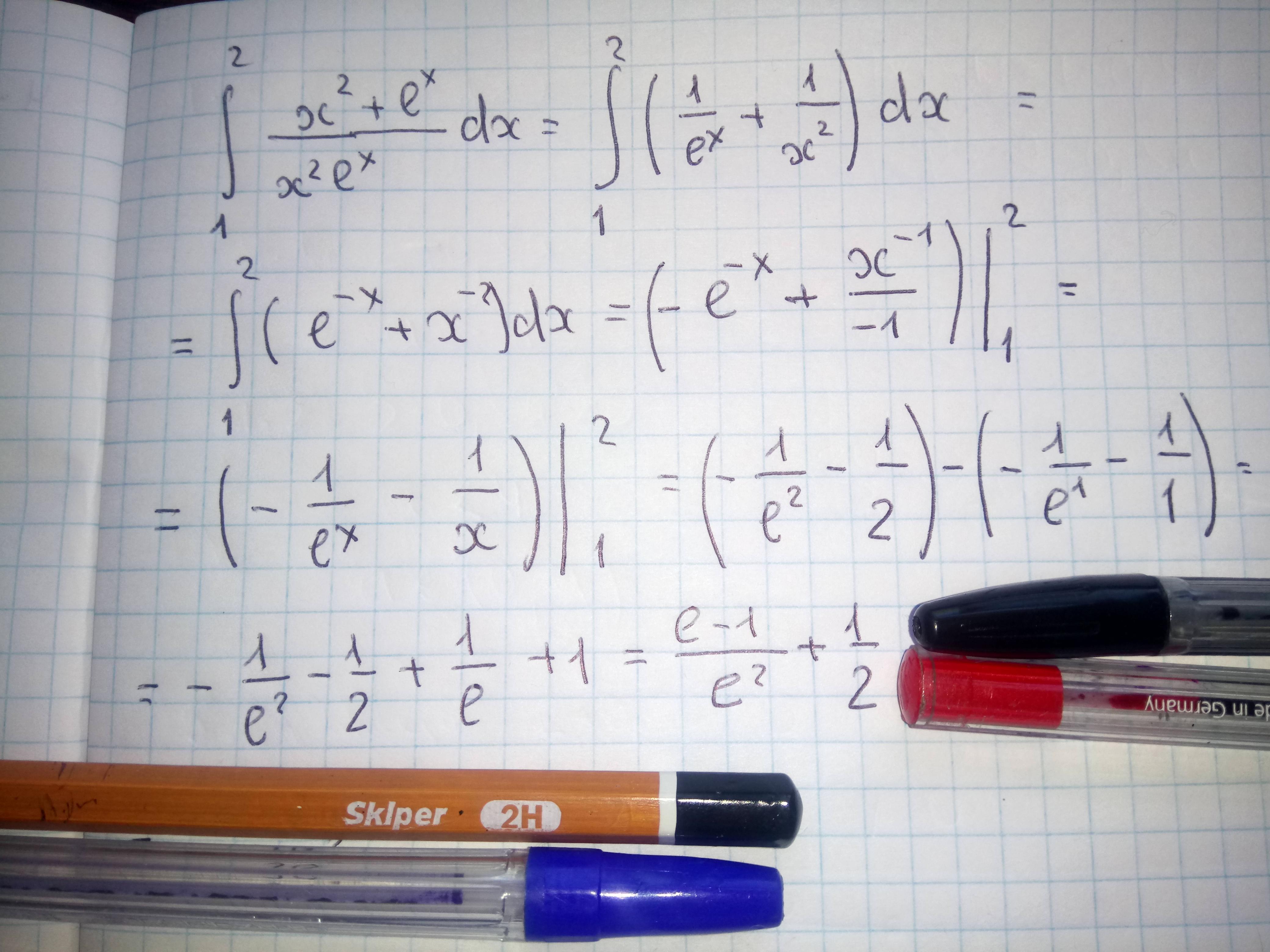
Похожие вопросы
Предмет: Английский язык,
автор: герман111112
Предмет: Русский язык,
автор: sofka121
Предмет: Другие предметы,
автор: Кристина1Бирова
Предмет: Русский язык,
автор: Joler1dkkf
Предмет: Русский язык,
автор: Симка2007