Предмет: Алгебра,
автор: asdq2780
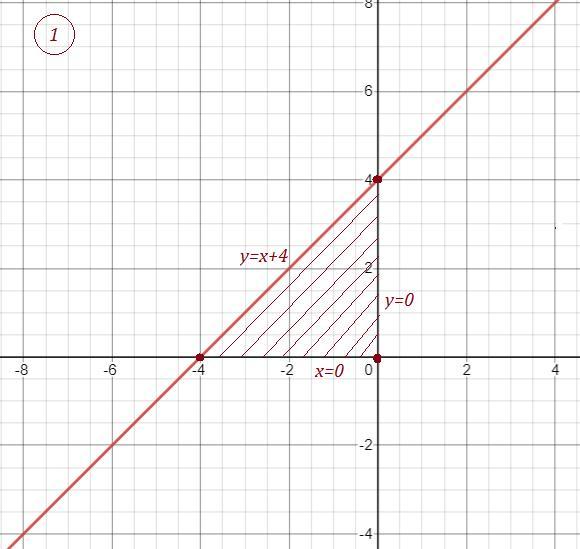
1) Вычислить площадь фигуры ограниченной линиями y=x+4 и осью ОХ и ОУ
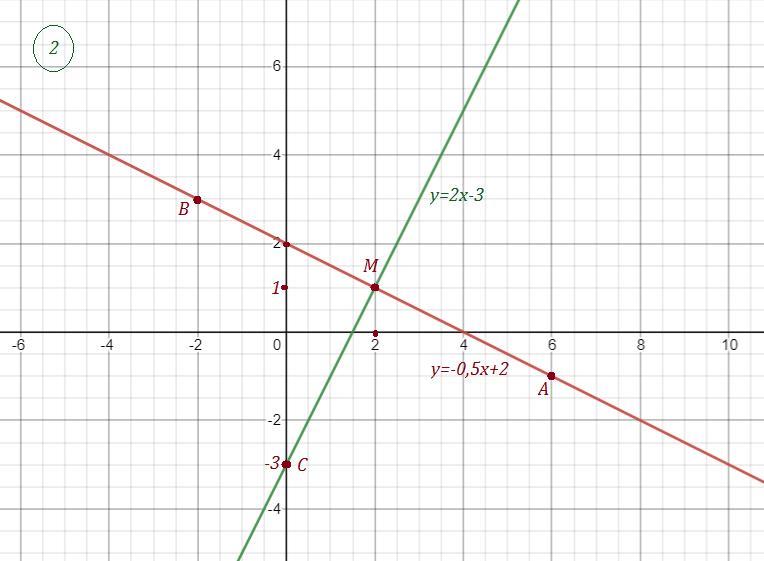
2) Найти точку С на оси ОУ, равно-удаленную от точек А(6,-1) и В(-2,3)
Ответы
Автор ответа:
0
Ответ:
Точка М(2;1) - середина отрезка АВ . Проведём прямую через точку М перпендикулярно АВ . На этом перпендикуляре все точки будут равноудалены от концов отрезка АВ .
Чтобы найти координаты точки С на оси ОУ, найдём точку пересечения перпендикуляра с осью ОУ (х=0) .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: арукаж
Предмет: Русский язык,
автор: 123318
Предмет: Русский язык,
автор: davron80
Предмет: Английский язык,
автор: evashatilo16
Предмет: Математика,
автор: nasty200655562