Предмет: Математика,
автор: katyajash
Решить интеграл, пожалуйста помогите :(
Приложения:
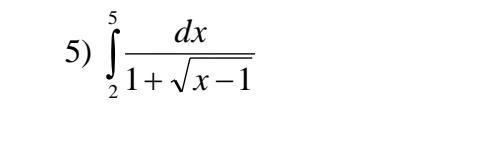
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:=
Cначала вычислим неопределённый интеграл:∫dx/(1+√(x-1))=
=|пусть x-1=t, тогда dx=dt|=
∫dt/√(t)+1=|пусть √t+1= u,⇒1/2√t dt=du, ⇒√t=u-1, dt=2√t·du|=2∫(u-1)du/u=
=2∫du- 2∫du/u=2(u- lnu)=2(√t+1 - ln(√t+1))=2√(x-1) - 2ln(√(x-1) +1) +C
=(2√(x-1) - 2ln(√(x-1) +1) |₂⁵= -2ln3+2ln2+2
Похожие вопросы
Предмет: Українська мова,
автор: oleksiy2002
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: viles151
Предмет: Математика,
автор: pandoragamer92
Предмет: Русский язык,
автор: 10472855