Предмет: Геометрия,
автор: gp5px3va9y
Найдите радиус окружности, касающейся сторон прямого угла, если наименьшее расстояние от вершины этого угла до окружности равно 13см
Ответы
Автор ответа:
4
Ответ: ≈31,38 см.
Объяснение:
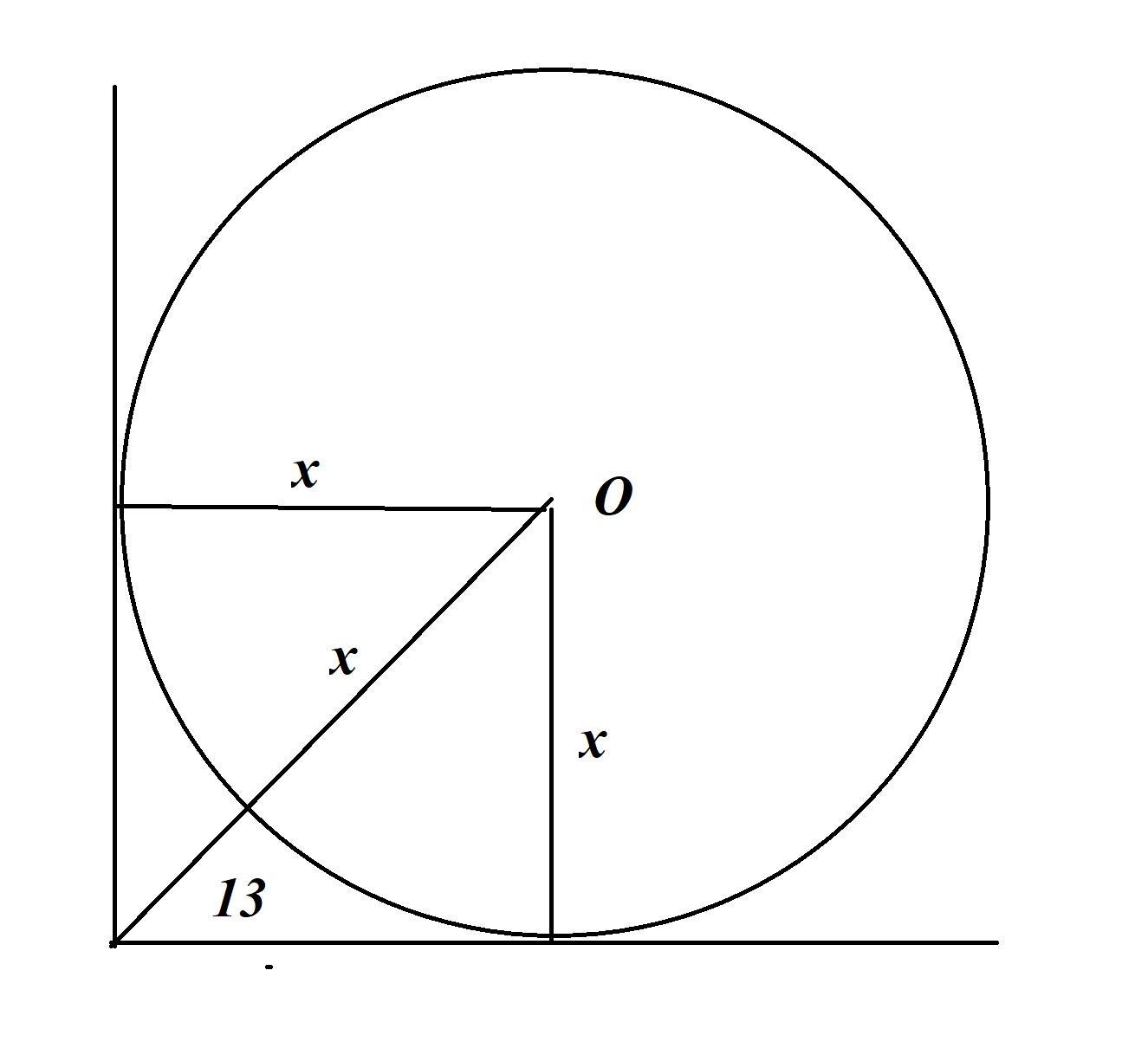
x см - радиус искомой окружности.
x+13 см - диагональ квадрата со стороной х см. Тогда по т. Пифагора
(x+13)²=2x²; (См. скриншот)
x²+26x+169=2x²;
x²-26x-169=0;
a=1; b=-26; c=-169;
D=b²-4ac=(-26)²-4*1*(-169)=676+676=1352>0 - 2 корня.
x1=(-b±√D)/2a=(-(-26)±√1352)/2*1=(26±26√2)/2=26(1±√2)/2=13(1±√2);
x1=13(1+√2)≈31,38 см.
x2=13(1-√2)≈-5.38 - не соответствует условию.
Радиус окружности равен ≈31,38 см.
Приложения:
gp5px3va9y:
Спасибо большое
Можно я закреплю одно задание здесь вы объясните пожалуйста
Найдите больший угол между касательными проведенными через концы хорды равной радиусу окружности
Похожие вопросы
Предмет: Русский язык,
автор: inn8aymelenaitali
Предмет: Другие предметы,
автор: olga338
Предмет: Русский язык,
автор: МиссАлис
Предмет: Русский язык,
автор: 556555665556
Предмет: Русский язык,
автор: Софьясова