Question

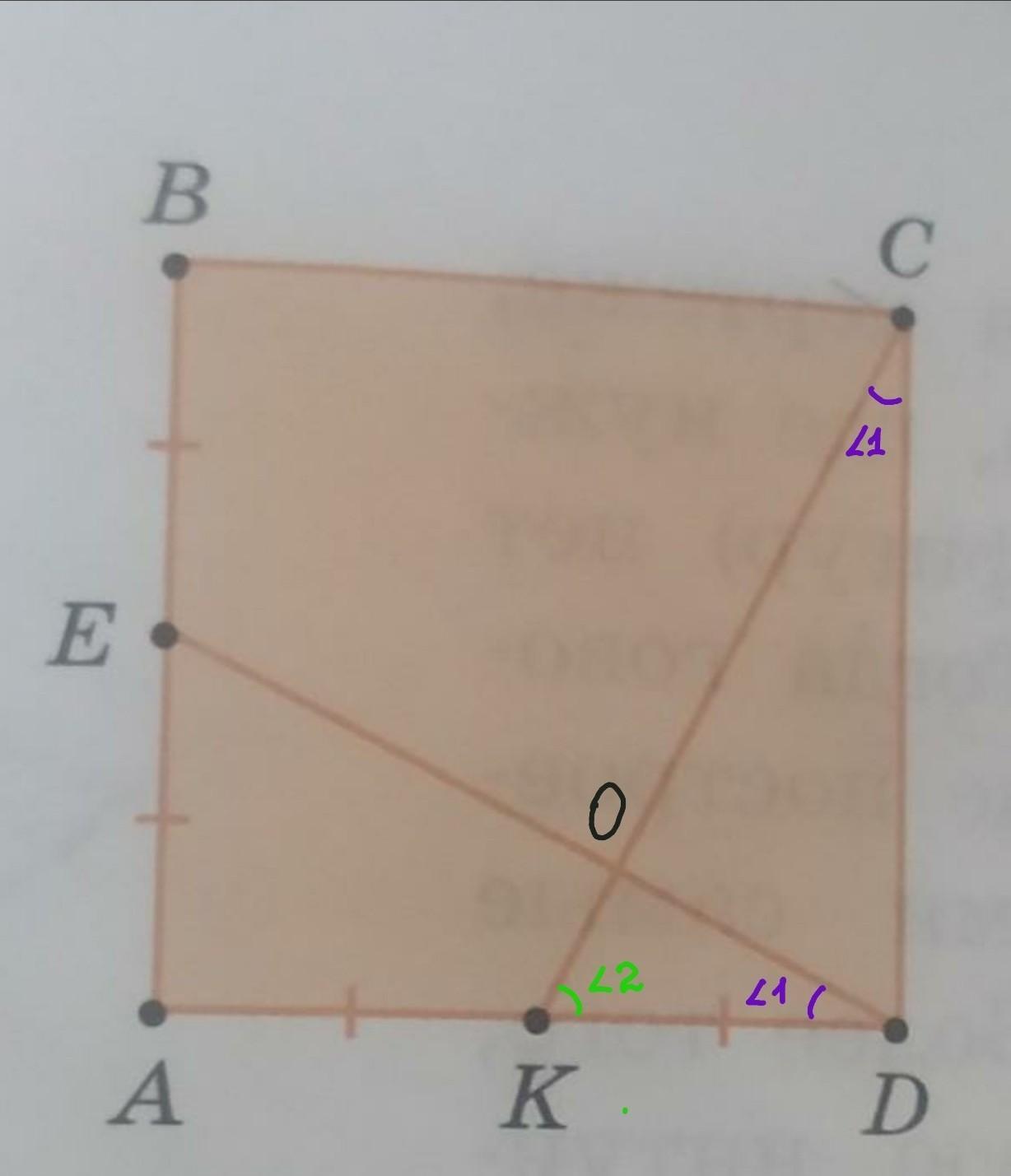
Точки Ки E - середины сторон квадрата.
ABCD. Докажите, что отрезки ски DE перпенди-
кулярны друг другу (рис. 15.7).
P​

Answer 1

Пошаговое объяснение:

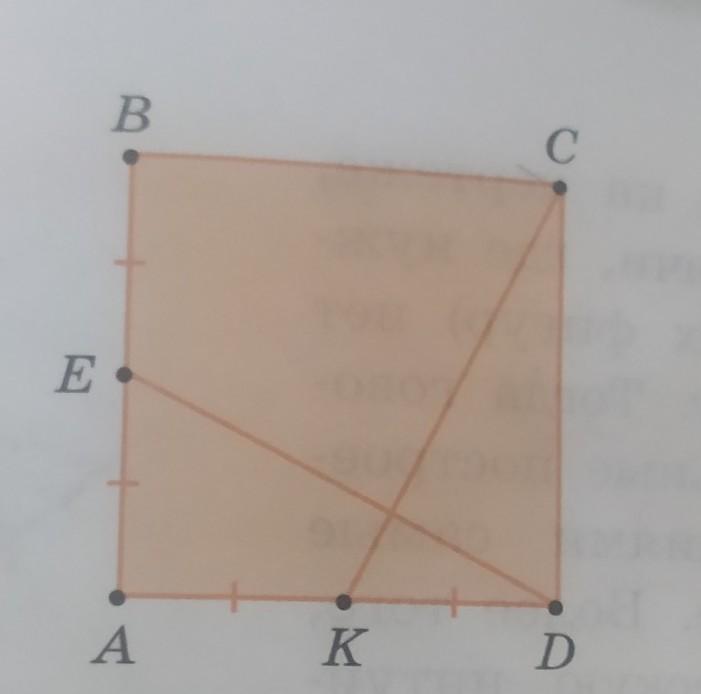
Точки К и E - середины сторон квадрата ABCD. AE=BE, AK=KD. Докажите, что отрезки DE и CK перпендикулярны друг другу.

У квадрата все стороны равны, следовательно и половины сторон квадрата равны между собой.

Пусть AE=BE=AK=KD=а, тогда AD=AK+KD=2a. CD=AD=2a, как стороны квадрата.

Рассмотрим прямоугольные треугольники ADE и DCK.

У них: АD=CD=2а, AE=KD=а. Треугольники равны по двум катетам.

Из равенства треугольников следует равенство углов: ∠KCD=∠EDA.

Рассмотрим △DCK.

Обозначим ∠KCD=∠1, а ∠CKD=∠2.

Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠1+∠2=90°.

Рассмотрим △ KOD.

Так как сумма углов треугольника равна 180°, то:

∠KOD=180°-∠1-∠2=180°-(∠1+∠2)=180°-90°=90°.

Если отрезки пересекаются под прямым углом, то они перпендикулярны друг другу: DE⟂CK, что и требовалось доказать.

#SPJ3