Предмет: Геометрия, автор: glebken1022

Помогите! Сто баллов! Мне нужно нормальное решение этой задачи!
В треугольнике CDE биссектрисы CK и EN пересекаются в точке P,

причём DP=6, ∠DE = 60°. Найдите расстояние от точки P до стороны

CE

Кто ответит - тому лучший ответ, сердечко и 100 баллов

glebken1022: Ребят пожалуйста

на знаниях уже есть решение но оно неправильное

Ответ:

∠CED = 24°

Треугольник CED: для простоты записи обозначим x половинки угла D и у - половинки угла С. Тогда

∠CED = 180 - 2х - 2у = 180 - 2(х + у)

∠DFK = 78° является внешним для ΔDCF, поэтому

∠DFK = х + у, то есть х + у = 78°

Тогда ∠CED = 180° - 2 · 78° = 24

тут даже найдено не то что надо

пожалуйста

MarinaSkorina: уточните точно какой угол равен 60 градусов. угол обозначается или одной или тремя буквами.

glebken1022: cde

glebken1022: простите, опечатался

MarinaSkorina: ок

glebken1022: Решите?

Ответы

Автор ответа: MarinaSkorina

Ответ:

Ответ в фото с решением. Удачи.

Приложения:

glebken1022: спасибо

Автор ответа: ужнеужели

Ответ:

Основное в этой задаче - доказательство того, что треугольник равносторонний. Остальное решается в одну строку.

Объяснение:

Приложения:

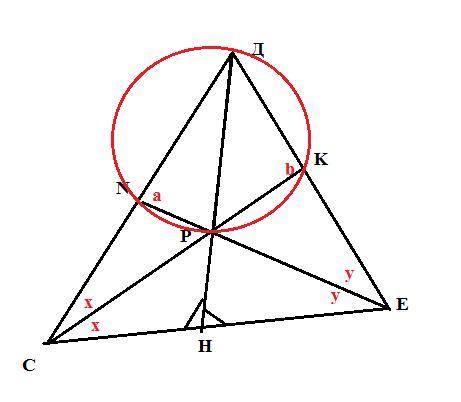
ужнеужели: Все можно решить проще. Вписать в треугольник окружность. Провести из точки Р к стороне СД или СЕ и так как он лежит против угла 30 градусов, то равен половине РД, то есть 3. Но это и есть искомое расстояние.

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: IlischanKhamkhoev

Как можно определить спряжение глагола?
1) По вопросу.
2) По форме третьего лица множественного числа.
3) По форме первого лица единственного числа.
4) По неопределенной форме.

1 год назад

Предмет: Қазақ тiлi, автор: Seinur16

помогите пожалуйста !!!

1 год назад

Предмет: Русский язык, автор: Аноним

Как пишется - держИм или держЕм

1 год назад