Предмет: Алгебра,
автор: Аноним
Интегралы. Помогите кто может, пожалуйсто!
Приложения:
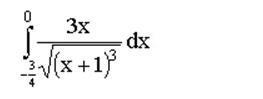
Ответы
Автор ответа:
1
Ответ:
Аноним:
спасибо большое! Вы лучшие!
тогда отмечай лучший ответ
ок, жду второго ответа и дам лучший)
галачки нема прост(
Похожие вопросы
Предмет: Русский язык,
автор: каквсавитььъ
Предмет: Русский язык,
автор: гай2
Предмет: Русский язык,
автор: veliva
Предмет: Математика,
автор: ulduzaskerova2