Предмет: Алгебра,
автор: katyatrunova1130
Вычислите интеграл 40 баллов!!
Приложения:
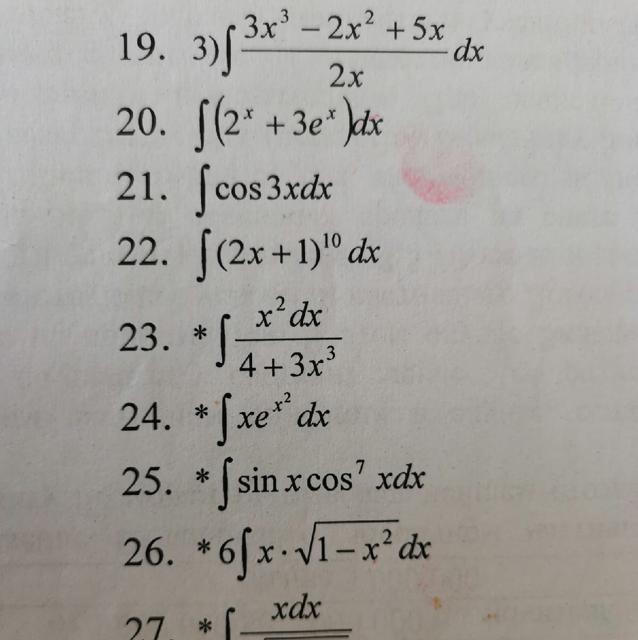
Zorbinaaa:
за 100
договорились?
Давай
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: yyyyyy77878
Предмет: История,
автор: figurelove12
Предмет: Русский язык,
автор: новичок508