Предмет: Алгебра,
автор: amkznxnsnwkksksksk
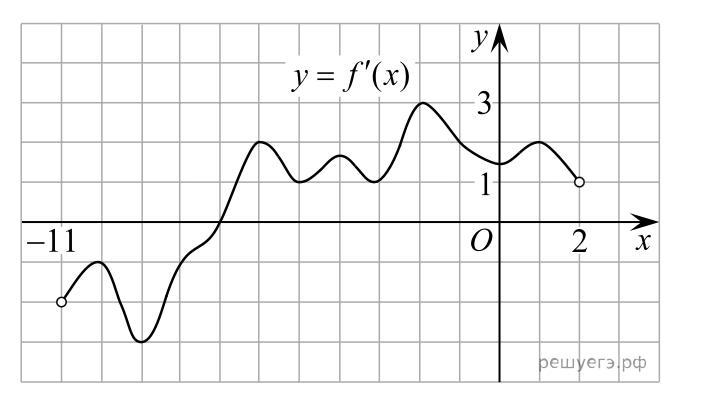
На рисунке изображён график y = f'(x) — производной функции f(x), определённой на отрезке (−11; 2). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней.
Подробно , пожалуйста
Приложения:
Ответы
Автор ответа:
1
Ответ:
-7
Объяснение:
Производная функции f(x) в точке х₀ - точке касания равна k - угловому коэффициенту касательной, т.е. f`(x₀)=k.
По условию, касательная параллельна оси Ох, значит, k=0, т.е. f`(x₀)=0.
По графику определяем, где f`(x₀)=0, т.е. где график y = f'(x) пересекает ось Ох. Это точка х₀=-7
Похожие вопросы
Предмет: Английский язык,
автор: маша483
Предмет: Русский язык,
автор: Аноним
Предмет: Немецкий язык,
автор: cristinakup
Предмет: Математика,
автор: аринаром
Предмет: Литература,
автор: liza5899