Предмет: Алгебра,
автор: fote1515
помогите найти предел пожалуйста! я не понимаю темы какой лучший способ решать??
Приложения:
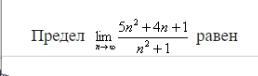
Ответы
Автор ответа:
2
Ответ:
5
Объяснение:
Вынесем в числителе и знаменателе наибольшую степень
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: enichca87
Предмет: Английский язык,
автор: ilvira791
Предмет: Русский язык,
автор: enichca87
Предмет: Математика,
автор: марина1596
Предмет: Русский язык,
автор: Mesedushka555