Question

На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=2x-2 или совпадает с ней.
Подробно , пожалуйста

Answer 1

Ответ:   $x_0=5$  .

Угловой коэффициент прямой  у=2х-2  равен  k=2 . Если касательная параллельна этой прямой или совпадает с ней , то их угловые коэффициенты равны.

Угловой коэффициент касательной к графику функции  y=f(x) равен значению производной в точке касания, то есть   $k=f'(x_0)$  .

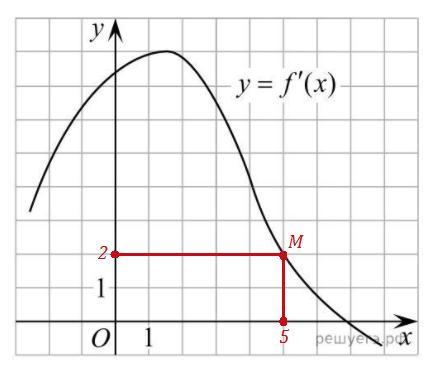
На оси ординат находим значение у=2, проводим прямую, параллельную оси ОХ, и находим на графике функции точку М  - точку пересечения графика с прямой у=2.

Далее Находим абсциссу точки М . Это и будет абсцисса точки, в которой касательная к графику функции y=f(x) параллельна прямой y=2x-2 или совпадает с ней.

Координаты точки М(5;2) , значит  $x_0=5$  .