Предмет: Алгебра,
автор: allayarabdullayev
{3√X+3√Y=5
{X+Y=35
Ps: выше кубические корни, это система, плиз с объяснением
Ответы
Автор ответа:
1
Решение задания прилагаю
Приложения:
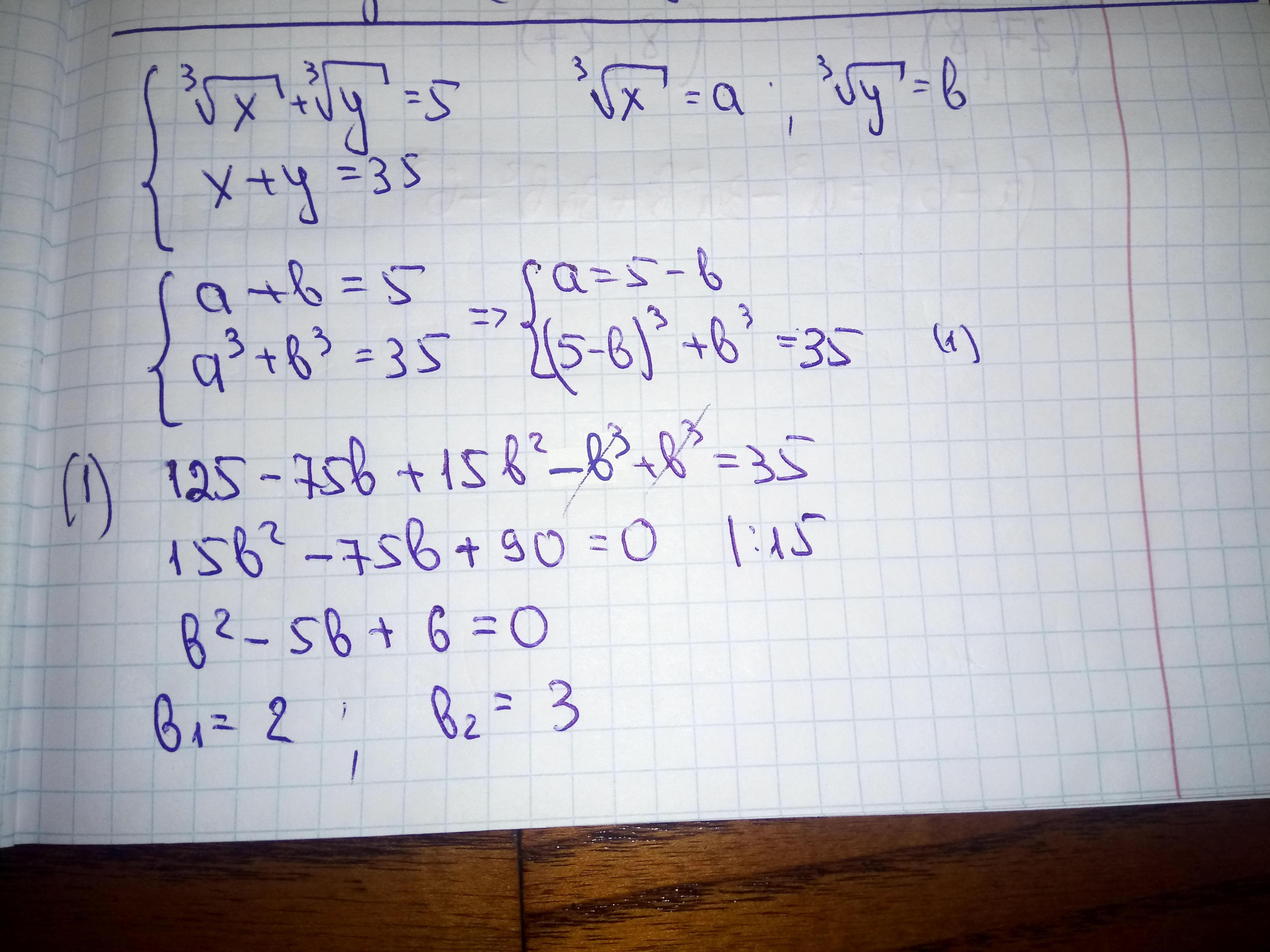

allayarabdullayev:
спасибо
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: NataliaKim
Предмет: Русский язык,
автор: лили63
Предмет: Другие предметы,
автор: NataliaKim
Предмет: Русский язык,
автор: zaxac075
Предмет: История,
автор: aleks1yus