Предмет: Алгебра,
автор: МяяУкОло
Исследовать сходимость знакопеременных рядов. Если ряд
сходится, то определить, сходится он абсолютно или условно.
Приложения:
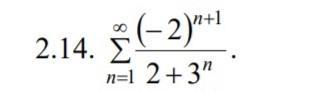
Artsounds:
он не сходиться, метод не применим
Ответы
Автор ответа:
1
Сходимость ряда
Признак сходимости знакочередующихся рядов (признак Лейбница):
Пусть имеется ряд
Тогда, если выполнены условия:
- Ряд является знакочередующимся.
- Члены ряда убывают по модулю
то ряд сходится.
1) Чередование знаков
Ряд является знакочередующимся, т.к. присутствует множитель
2) Убывание по модулю
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
Таким образом, ряд сходится
Тип сходимости
Сходящийся ряд называют абсолютно сходящимся, если сходится ряд
.
Сходимость такого ряда можно определить с помощью предельного признака Даламбера
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
Ряд сходится по признаку Вейерштрасса, следовательно исходный ряд сходится абсолютно.
Похожие вопросы
Предмет: Английский язык,
автор: Katykate15
Предмет: Английский язык,
автор: viktoriy991
Предмет: Русский язык,
автор: Minion307
Предмет: Другие предметы,
автор: dashakovalenko0