Найдите A и B, при которых f(x) делится на g(x) без остатка.
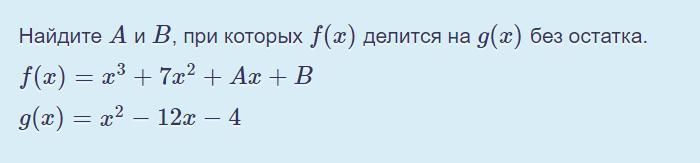
Ответы
Ответ:
Объяснение:
1) Разделим f(x) на g(x) в столбик
2) Остаток от деления приравняем к 0
3) Решим уравнение методом неопределенных коэффициентов
1)
x³+7x²+Ax+B I x²-12x-4
-x³+12x²+4x I x+19
= 19x²+(A+4)x+B
-19x²+228x+76
= x(A+232)+B+76
2) x(A+232)+(B+76)=0
3) x(A+232)+(B+76)=0
A+232=0 ; A=-232
B+76=0 ; B=-76
Ответ A=-232 B=-76
Ответ: A = - 32 ; B = - 76 .
Объяснение:
f(x) = x³ + 7x² + Ax + B ; g(x) = x² - 12x - 4 ; A - ? B - ?
Нехай при діленні f(x) на g(x) націло частка буде двочлен х + С , тоді
f(x) = ( х + С ) * g(x) ; розкриємо дужки і прирівняємо коефіцієнти :
x³ + 7x² + Ax + B = ( х + С )* ( x² - 12x - 4 ) ;
x³ + 7x² + Ax + B = x³ - 12x² - 4x + Cx² -12Cx - 4C ;
{ - 12 + C = 7 , C = 7 + 12 = 19 ;
{ - 4 - 12C = A , A = - 4 - 12* 19 = - 4 - 228 = - 232 ;
{ -4C = B ; B = - 4 * 19 = - 76 .