Предмет: Математика,
автор: xolodok33331
Найти полные дифференциалы следующих функций
Приложения:
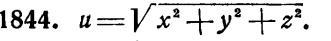
Ответы
Автор ответа:
1
Ответ: на фото
Пошаговое объяснение:
На фото
Приложения:
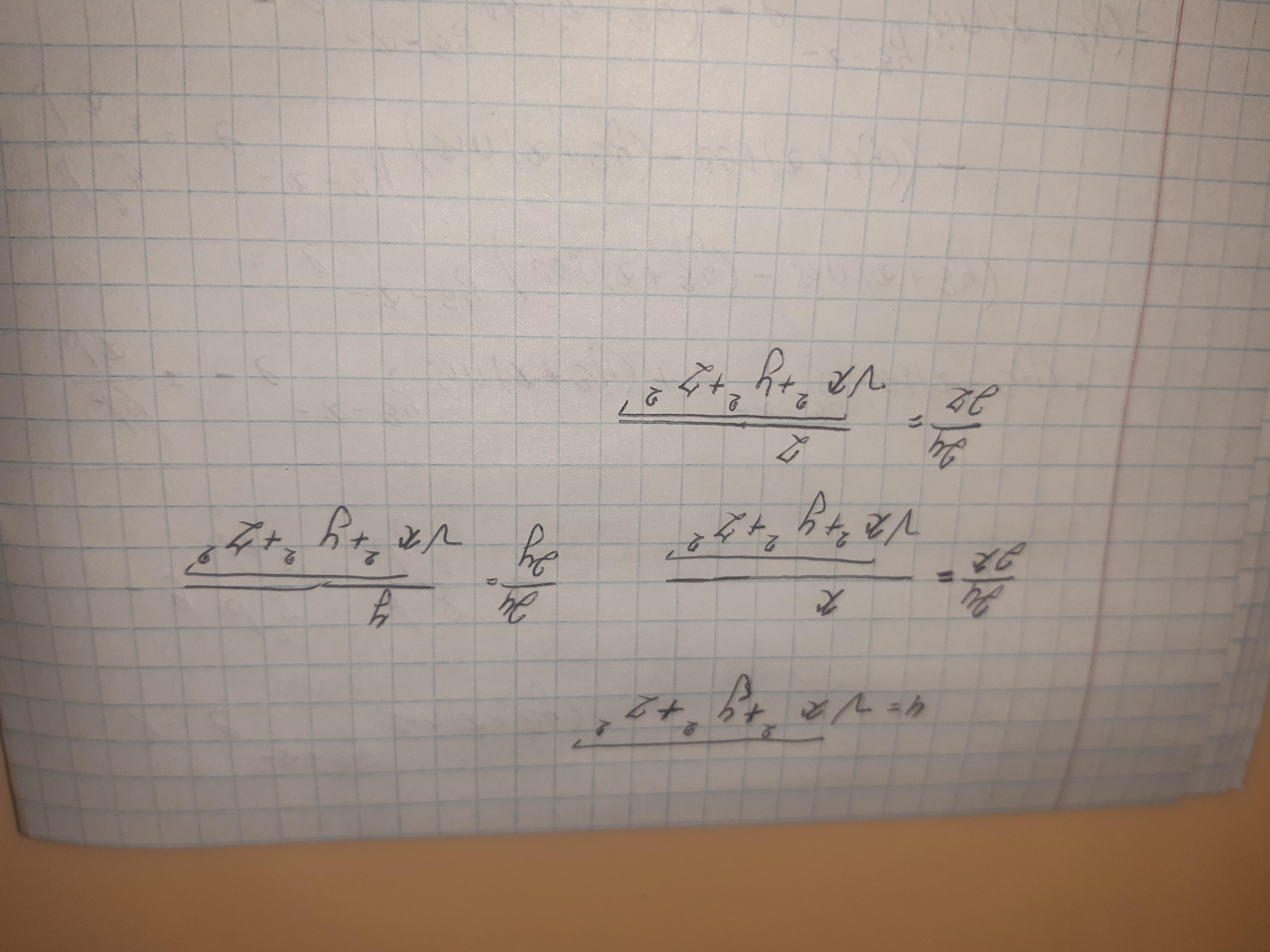
Miroslava227:
это не дифференциал
вы просто производные нашли
Все время путаю их
Автор ответа:
0
Ответ:
Формула полного дифференциала:
собираем:
Похожие вопросы
Предмет: Русский язык,
автор: zhiva181004
Предмет: Русский язык,
автор: missgene4ka
Предмет: Русский язык,
автор: Tatk83a
Предмет: Математика,
автор: Krasavchyk
Предмет: Математика,
автор: antomimik