Предмет: Математика,
автор: xolodok33331
Найти du/dt, если, задача представлена в картинке ниже
Приложения:
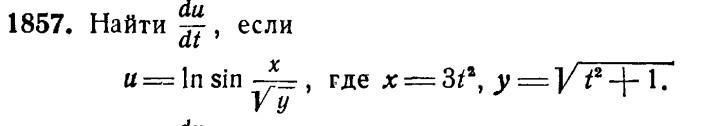
Ответы
Автор ответа:
0
Формула:
собираем производную:
Похожие вопросы
Предмет: Русский язык,
автор: vikhrovaanna
Предмет: Русский язык,
автор: slaider2004
Предмет: Английский язык,
автор: Anna6911
Предмет: Физика,
автор: KejVan
Предмет: Русский язык,
автор: dianamelnik59