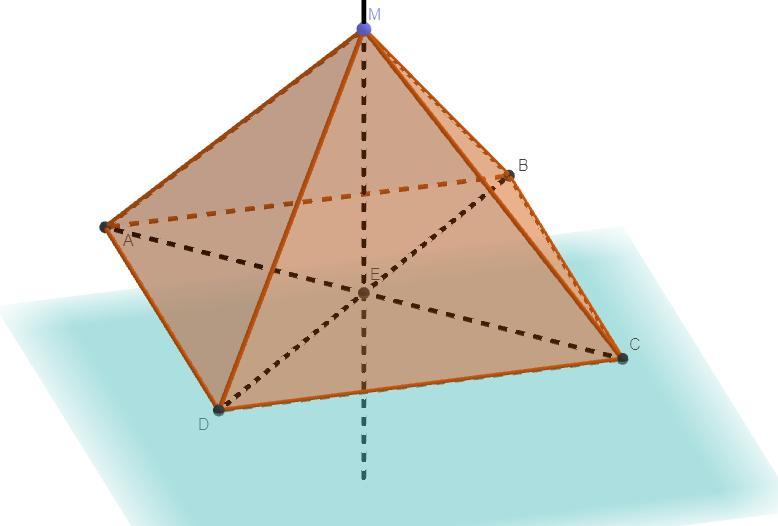
Боковое ребро правильной четырехугольной пирамиды MABCD с вершиной M равно стороне ее основания. Найдите угол между прямыми AB и CM.
очень срочно, завтра зачёт
Ответы
Ответ:
∠(AB,CM) = 60°
Объяснение:
Дано: MABCD - правильная четырехугольная пирамида, MD = DC
Найти: ∠(AB,CM) - ?
Решение: По определению пирамиду называют правильной если, её основание правильный многоугольник, а высота пирамиды является центром этого многоугольника. Правильным четырехугольником является квадрат. По определению угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, которые соответственно параллельны заданным скрещивающимся прямым, тогда так как ABCD - квадрат, то AB ║ DC, следовательно ∠(AB,CM) = ∠(MD,DC) = ∠MDC .Пусть диагонали квадрата пересекаются, в точке E. Точка пересечения диагоналей квадрата является центром квадрата. Треугольник ΔMED и ΔMEC - прямоугольны так как ME - высота пирамиды, следовательно ΔMED = ΔMEC по двум катетам так как ME - общая и делит диагонали на четыре равны отрезка по свойству квадрата, тогда DE = EC. ΔMED = ΔMEC ⇒ MD = MC, а так как по условию MD = DC, то MD = MC = DC и треугольник ΔMDC - правильный, тогда по свойству правильного треугольника каждый его угол 60° и ∠MDC = ∠(AB,CM) = ∠(MD,DC) = 60°.