Предмет: Алгебра,
автор: Jackoe89
Решить дифференциальное уравнение y" + 2y' + y = (e^-x)/(x sqrt(x))
Приложения:
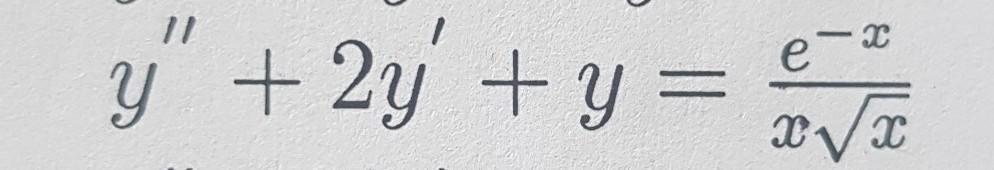
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Характеристическое уравнение:
k^2 + 2k + 1 = 0
k1 = k2 = -1
y0 = (C1 + C2*x)*e^{-x}
В правой части стоит e^{-x}, и при этом -1 - корень характеристического уравнения, да еще и кратный (двойной). Поэтому частное решение:
Решаем неоднородное уравнение
Подставляем в уравнение:
Сокращаем e^(-x) и приводим к общему знаменателю 4x√x:
Избавляемся от знаменателя:
A(4x^2 - 4x - 1) + 2A(2x - 4x^2) + 4Ax^2 = 4
4Ax^2 - 4Ax - A + 4Ax - 8Ax^2 + 4Ax^2 = 4
-A = 4
A = -4
y* = -4√x*e^(-x)
В итоге
y = y0 + y* = (C1 + C2*x)*e^{-x} -4√x*e^(-x) = (C1 + C2*x - 4√x)*e^(-x)
Похожие вопросы
Предмет: Русский язык,
автор: витя2006
Предмет: Қазақ тiлi,
автор: Родион241
Предмет: Английский язык,
автор: Pavelhel
Предмет: Русский язык,
автор: ahmadullinismap7oxh7
Предмет: Биология,
автор: nissansuper3