Предмет: Математика,
автор: Childebaev86
решите неравенство log 1-x (x + 2)<1
Приложения:
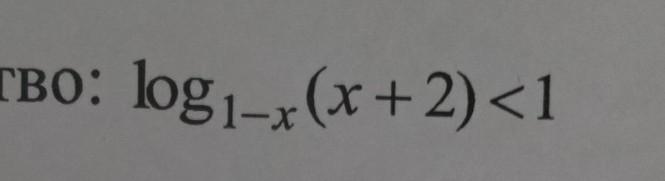
Ответы
Автор ответа:
3
ОДЗ:
1-x ≠ 1
x ≠ 0
x ∈ (-2;0) ∪ (0 ; 1)
Теперь рассмотрим два случая:
1)
при
монотонно возрастает, соответственно мы имеем право опустить логарифмы без изменения знака неравенства
x ∈ ( -∞ ; -)
2)
при
монотонно убывает, соответственно мы имеем право опустить логарифмы, изменив знак неравенства.
x ∈ (0 ; 1)
Теперь осталось пересечь наши решения с ОДЗ:
x ∈ ( -2 ; ) ∪ ( 0 ; 1 )
Ответ: x ∈ ( -2 ; ) ∪ ( 0 ; 1 )
UPD: знаю, что можно было решить намного проще с помощью метода рационализации, но почему-то не все учителя принимают его, поэтому я расписал классическим способом
Автор ответа:
1
Ответ: -2<х<-1/2, см фото.
Пошаговое объяснение:
Приложения:
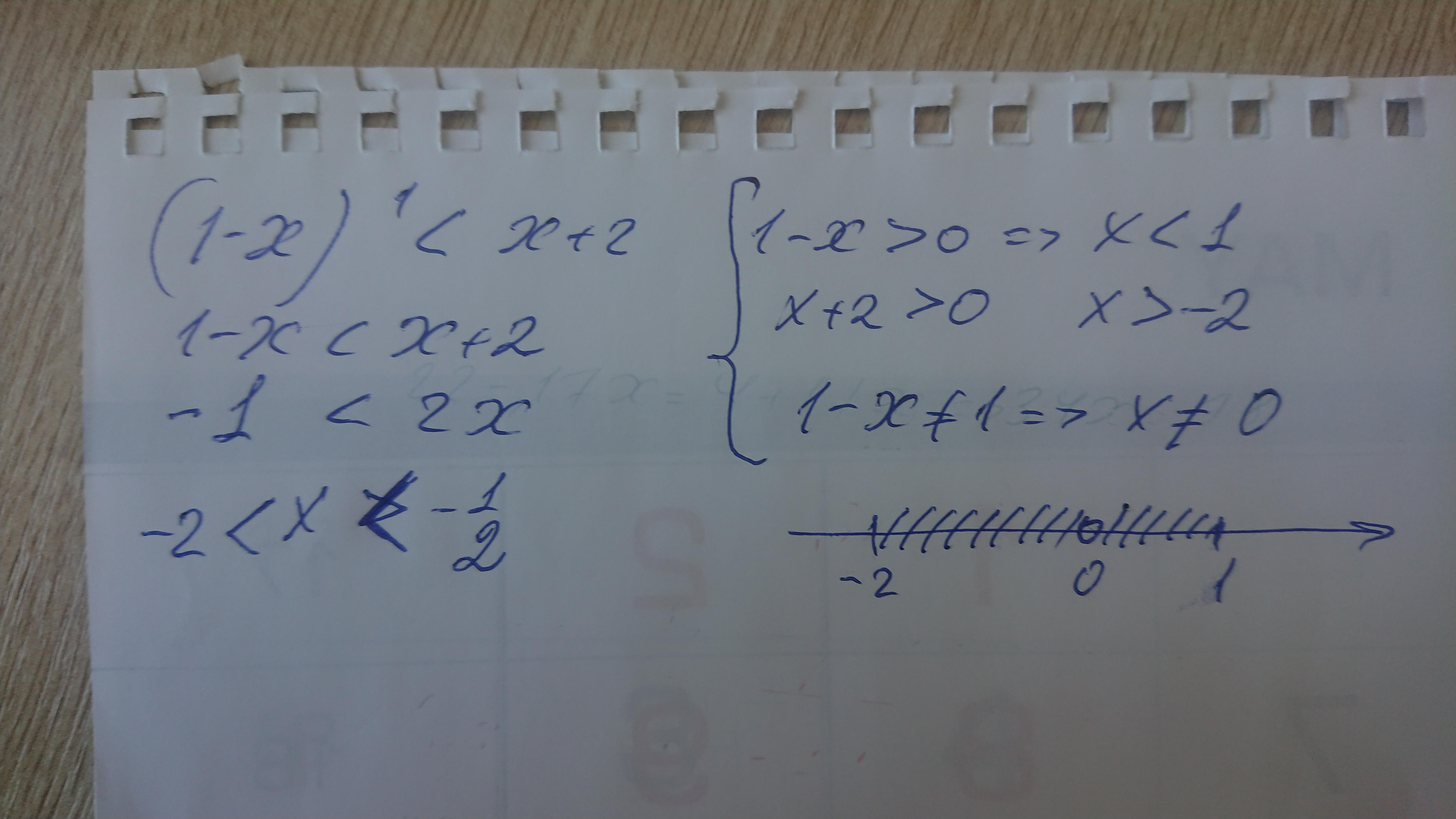
Похожие вопросы
Предмет: Русский язык,
автор: TIMACHKA
Предмет: Українська мова,
автор: Бодянович
Предмет: Русский язык,
автор: zhanakondel
Предмет: Физика,
автор: dasew12
Предмет: Литература,
автор: СашаЖданов