Предмет: Геометрия,
автор: Victor1a64
Бічна сторона рівнобічної трапеції дорівнює 6√3 см, а тупий кут 120°. Знайти площу трапеції, якщо
відомо, що в неї можна вписати коло.
Ответы
Автор ответа:
2
Ответ:
54√3 см²
Объяснение:
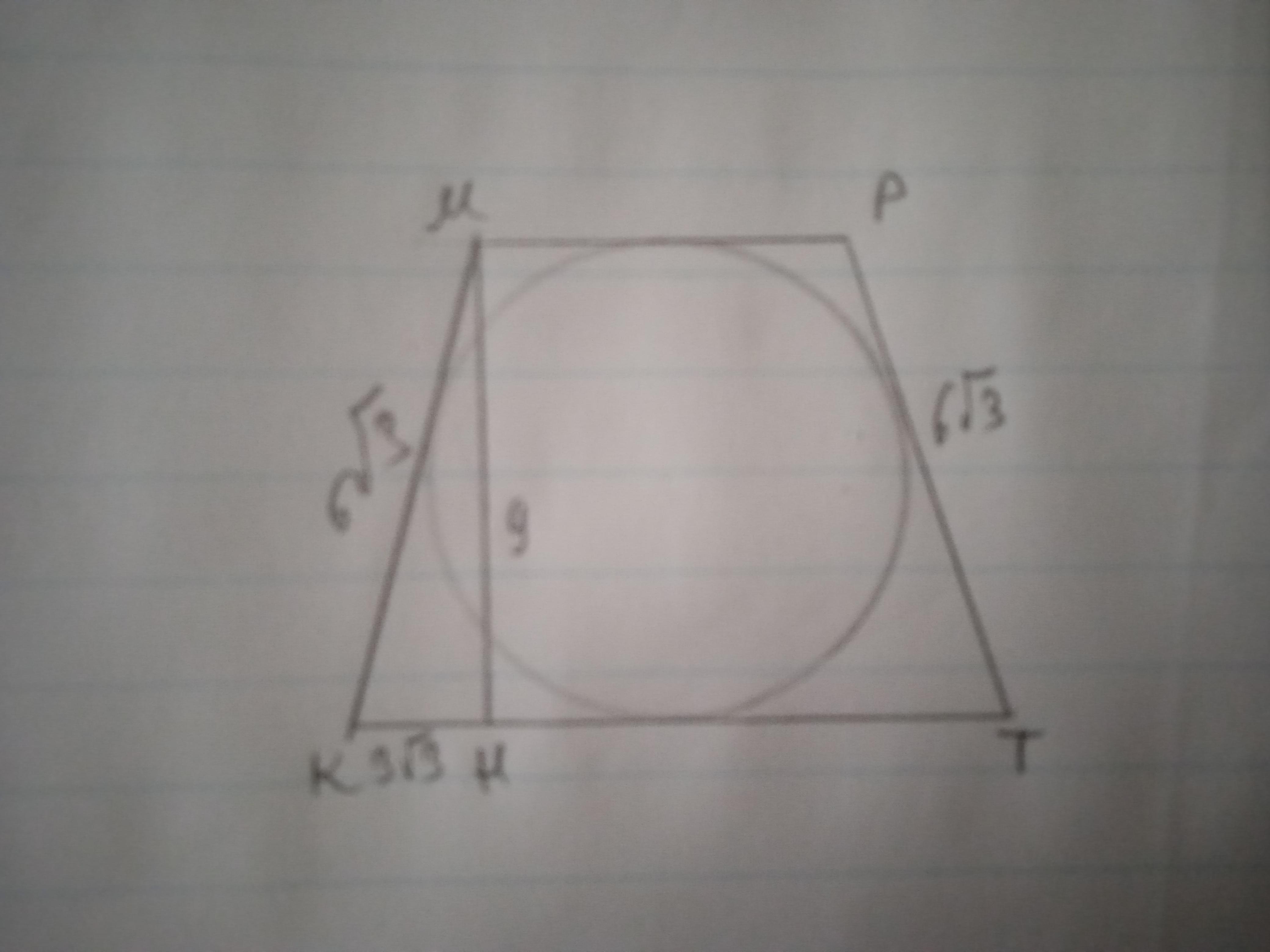
Дано: КМРТ - трапеція, КМ=РТ=6√3 см, ∠М=∠Р=120°. Знайти S(КМРТ).
Якщо навколо трапеції можна описати коло, сума основ дорівнює сумі бічних сторін.
КТ+МР=6√3+6√3=12√3 см.
Опустимо висоту МН, розглянемо ΔКМН - прямокутний.
∠КМН=120-90=30°, отже КН=1/2 КМ=3√3 см.
За теоремою Піфагора МН=√(6√3)²-(3√3)²=√(108-27)=√81=9 см.
S=(МР+КТ):2*МН=6√3 * 9 = 54√3 см²
Приложения:
Victor1a64:
СПАСИБО
Похожие вопросы
Предмет: Русский язык,
автор: see99aa
Предмет: Окружающий мир,
автор: паник1
Предмет: Русский язык,
автор: varvara20051
Предмет: История,
автор: eiline246
Предмет: Математика,
автор: Среднознайшик