Предмет: Математика,
автор: DedAAVT
50 баллов!
Найти производные функции
Приложения:
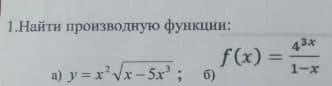
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
_________________________________________________________
Похожие вопросы
Предмет: Английский язык,
автор: alina480
Предмет: Английский язык,
автор: dostupzakrit
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: макс3394
Предмет: Окружающий мир,
автор: Зефирушки