задача 2
с объяснением !!!!!!!!!!!!!!!!!

Ответы
Ответ:
Объяснение:
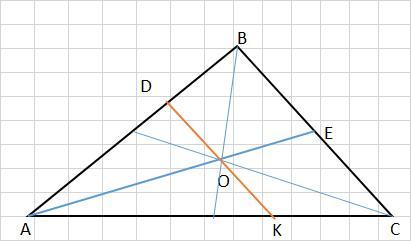
1) Рассмотрим ΔАВЕ и ΔАDО.
DK ║BC, следовательно,
∠АDO = ∠АВЕ как соответственные, ∠ВАЕ - общий. Значит,
ΔАВЕ ~ ΔАDО по 2-м углам. Тогда
ВЕ : DО = АЕ : АО (1)
Но АЕ - медиана ΔАВС.
А все три медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Значит, АО : ОЕ = 2 : 1 , т.е. АЕ составляет 3ч., следовательно,
АЕ : АО= 3 : 2 Подставляя это выражение в равенство (1), получим:
ВЕ : DО = 3 : 2, но ВЕ = ВС/2 = 15/2 = 7,5 (см) (т.к. АЕ - медиана)
7,5 : DO = 3 : 2, откуда
DO = 7,5 *2/3 = 2,5 * 2 = 5 (см)
2) Ааналогично: ΔАЕС ~ΔАОК по двум углам и
ЕС : ОК = АЕ : АО = 3: 2
ОК = 7,5 *2 / 3 = 5(см), т.е.
Медиана АЕ ΔАВС является и медианой(АО) ΔADK
3)DK = 5 * 2 = 10(см)
4) ΔАВС ~ ΔADK по 2 углам .
Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:
S(ΔABC) : S (ΔADK) = ВC² : DK² = 15² : 10² = 225/100 = 9 : 4
Ответ:
Объяснение:
Дано:
∆АВС
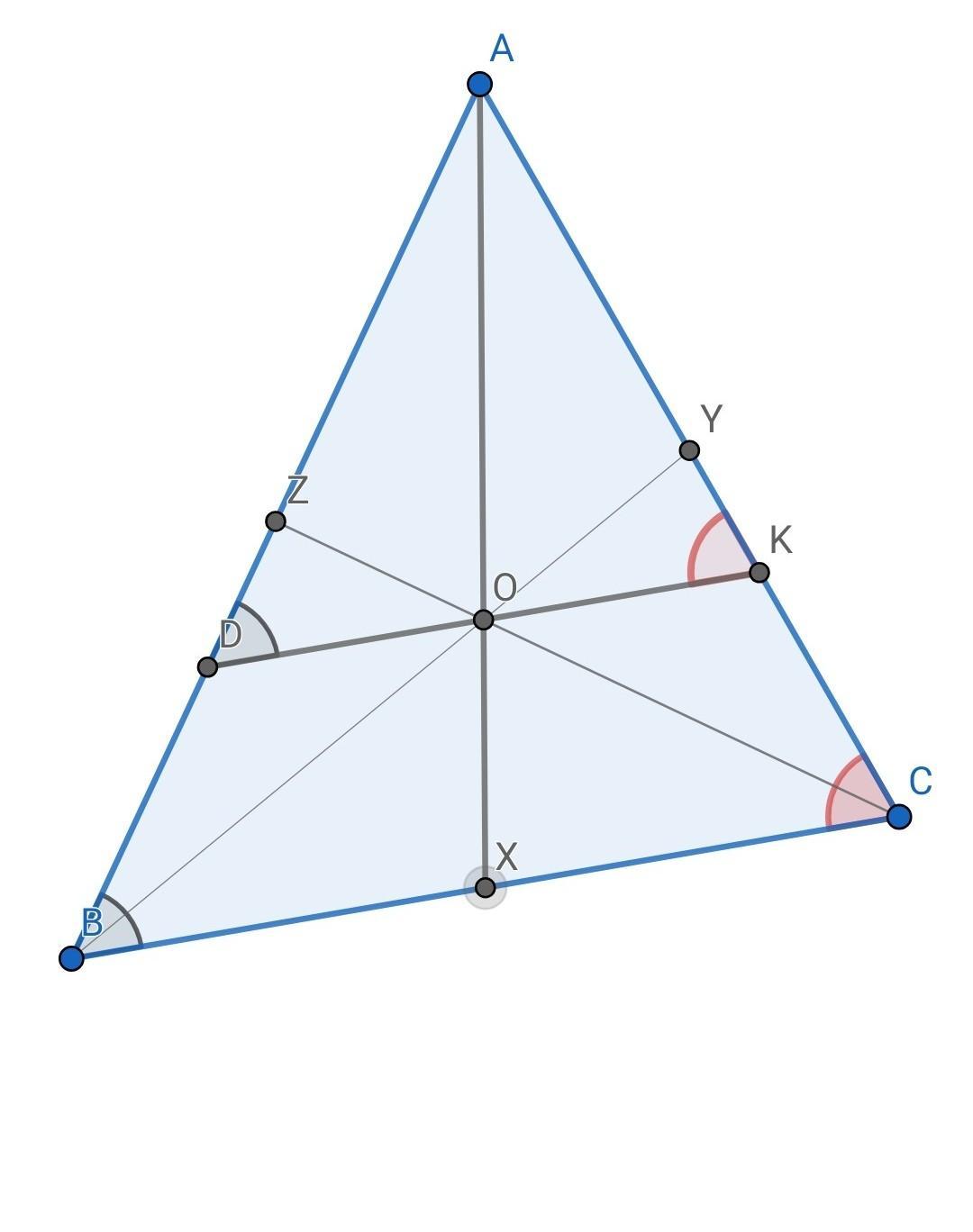
АХ, ВУ, СZ - медианы в ∆АВС
(AY=CY, AZ=BZ, BX=CX)
Решение:
Медианы треугольника пересекаются в одной точке, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Следовательно, получаем:
AO : OX = 2 : 1 => AO = 2•OX или OX = 0,5•AO;
AX = AO + OX => AX = AO + 0,5•AO = 1,5•AO
AX = 1,5•AO
Из условия: DK || BC => стороны АВ и АС треугольника можно рассматривать как секущие при 2 параллельных DK и ВС. => следующие углы равны как соответственные:
уг.АВС = уг.АDK;
уг.АСВ = уг.АKD.
=> ∆АВС подобен ∆АDK по 2м углам, а значит соотношение любых соответствующих линейных элементов в данных ∆ках одинаково и равно коэффициенту подобия =>
=> ВС / КD = АХ / AО = k
Но мы уже вычислили, что AX = 1,5•AO =>
АХ / АО = 1,5 => k = 1,5;
ВС / КD = 1,5 => KD = BC/1,5
BC = 15 => KD = 15/1,5 = 10
ВС = 10 см
Также у подобных треугольников соотношение площадей равно квадрату коэффициента подобия:
Ответ: