пожалуйста помогите решить (даю 20 баллов)
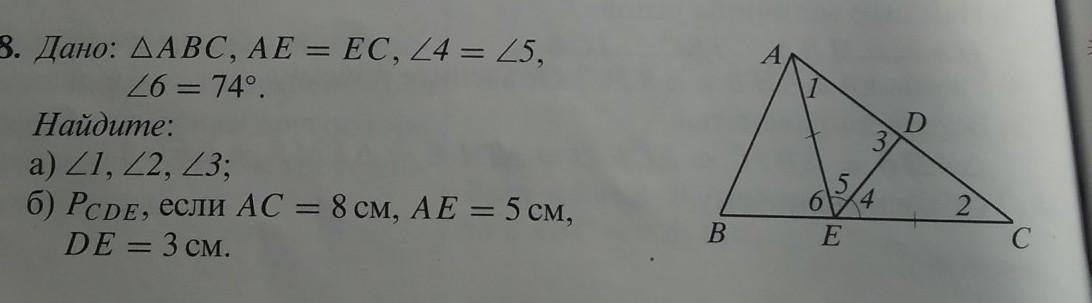
Ответы
Ответ:
........
Объяснение:
Рассмотрим треугольник АЕС:
ЕД-биссектриса, так как делит угол Е пополам на два равных угла. Так как АЕ=ЕС, треугольник АЕС-равнобедренный. По свойству мы знаем, что биссектриса равнобедренного треугольника является медианой и высотой.
Угол АЕВ=74° и угол АЕС-смежные. Сумма смежных углов равна 180°. Угол АЕС=180°-74°=106°
Угол Е при вершине треугольника АЕС равен 106°. Найдём общую сумму углов при основании. Угол ЕАС+угол АСЕ=74°. Найдём отдельно углы при основании. Угол ЕАС=углу АСЕ=74°:2=37°
Угол ЕДА=90°, так как ЕД-высота.
Угол АЕС=106°, ЕД-биссектриса, отсюда следует, что угол АЕД=углу ДЕС=106°:2=53°
ЕД-медиана, отсюда следует, что сторона ДС=АС:2, так как медиана делит сторону на две равны стороны. ДС=8:2=4
АЕ=ЕС=5;
Найдём по теореме Пифагора ЕД-катет прямоугольного треугольника СДЕ, так как угол СДЕ=90°
ЕД^2=СЕ^2-СД^2
ЕД^2=5^2-4^2=9
ЕД=3
Периметр это сумма всех сторон.
Р∆СДЕ=3+5+4=12
Ответ:
а) ∠1=37° ∠2=37° ∠3=90°
б) = 15см
Объяснение:
Если угол ∠6 равен 74°, то сумма углов ∠4 и ∠5 равна 180°-74°. То есть 106°. Так как ∠4 и ∠5 равны, то ∠4 (или ∠5) равен
106°÷2=53°
AE и EC равны, значит треугольник Δ AEC равнобедренный, а значит ∠1 и ∠2 тоже равны. Есть правило что сумма всех углов у треугольник равна 180°. Значит из 180° можно вычесть сумму ∠4 и ∠5 (106°) и получить сумму ∠1 и ∠2.
180°-106°=74°
74°÷2=37°
37° это угол ∠1 (или ∠2)
Осталось найти только угол ∠3
Так как треугольник Δ AEC равнобедренный то биссектриса угла (∠4+∠5) является его и высотой и медианой. А раз это высота то значит и угол ∠3 равен 90°
= DE+EC+DC
DE=3см AC=8см AE=5см
AC=EC
= 3+8+DC
DE медиана значит
DC=AC÷2
DC=4
= 3+8+4=15см