Предмет: Алгебра,
автор: passsiiive
Упростить пример по тригонометрии, девятый класс
Приложения:
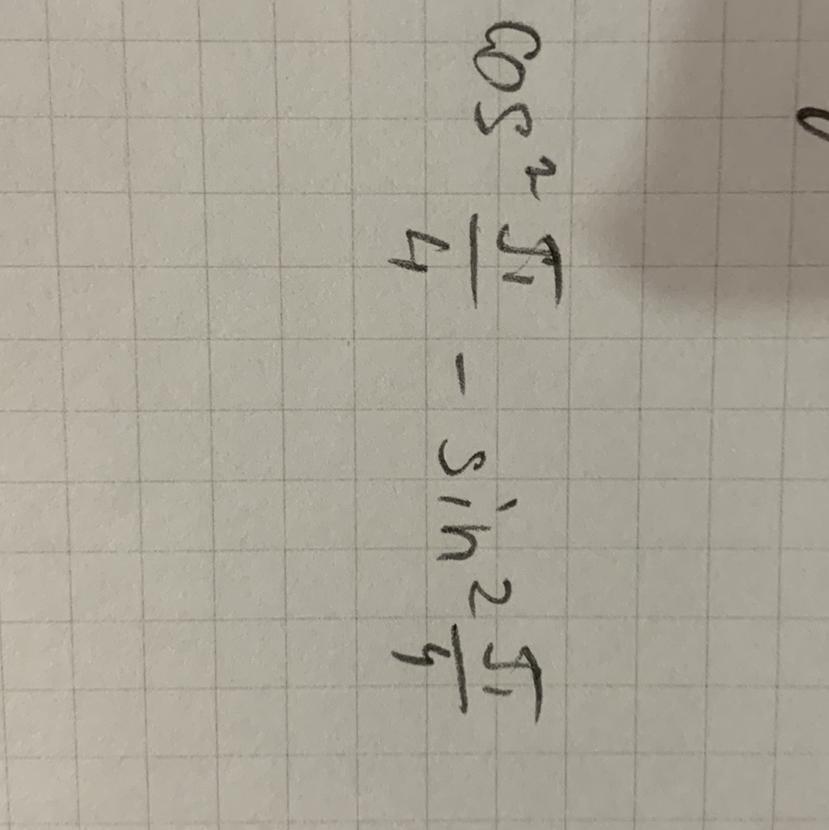
Ответы
Автор ответа:
1
1 способ (пользуясь известными значениями тригонометрических функций)
Поскольку и
эквивалентно выражениям
и
соответственно, то
2 способ (используя формулу)
Поскольку то
Ответ: 0.
Похожие вопросы
Предмет: Русский язык,
автор: MascentoIna0stina
Предмет: Русский язык,
автор: eminmusaev
Предмет: Русский язык,
автор: F1a1ntnashkoumn
Предмет: Алгебра,
автор: richi7
Предмет: Другие предметы,
автор: yana1562