упростите выражение
помогите пжпжпжп
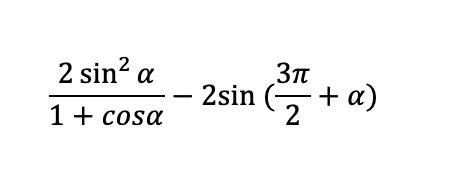
Ответы
Ответ:
Объяснение:
Разберем данное выражение по частям, начнем с левой дроби:
Для упрощения данной дроби вспомним одно из основных тригонометрических тождеств. Откуда выражая
получим:
. Подставим в нашу дробь:
Теперь разберем числитель дроби. В скобках заключена разность квадратов:
Имеем право сократить как в числителе, так и в знаменателе, получаем:
. (1)
Теперь рассмотрим вторую часть выражения:
Существует формула суммы углов для синуса:
Применим ее для нашего синуса:
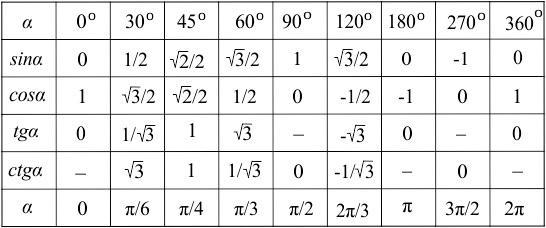
это синсус 270 градусов, т.к. "Пи" равно 180 градусам. По таблице тригонометрических функций (приложена во вложении) данный синус равен -1.
это косинус 270 градусов. По таблице тригонометрических функций данный косинус равен 0. Тогда возвращаясь в выражение выше:
(2)
Вернемся в изначальное выражение, используя (1) и (2):
.
Мы упростили выражение.