Предмет: Математика,
автор: momofjesus
нужно найти 2ю производную
Приложения:
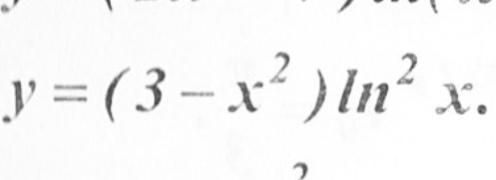
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Окружающий мир,
автор: софа110
Предмет: Окружающий мир,
автор: софа110
Предмет: Русский язык,
автор: KristinaDressen
Предмет: Литература,
автор: like92
Предмет: Қазақ тiлi,
автор: Kristino4kaMiy