Предмет: Математика,
автор: temkalololo
Найти cos a,если sin a
Приложения:
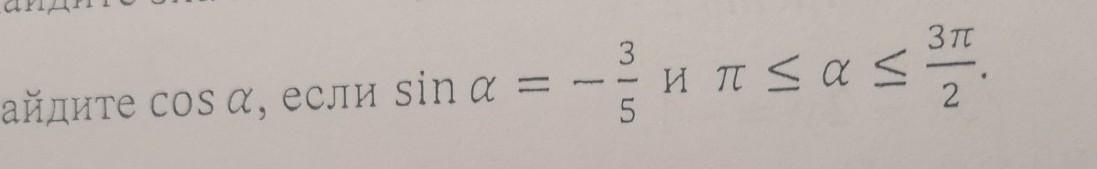
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Т.к π≤α≤3π/2, косинус будет будет отрицательный
Автор ответа:
0
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: karinagilmshin
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Токтаубек
Предмет: Геометрия,
автор: nik150307
Предмет: Биология,
автор: bsbsididndjsoappa