Задано линейное неоднородное дифференциальное уравнение
второго порядка с постоянными коэффициентами. Найти частное решение,
которое удовлетворяет приведенным начальным условиям.
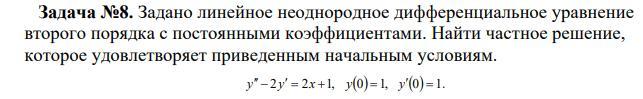
Ответы
Відповідь:
у=1/2+1/2е^2х-1/2х^2-х
Покрокове пояснення:
у"-2у'=0
р^2-2р=0
р1=0; р2=2
у=С1+С2×е^2х
у(0)=1; у'(0)=1
у(0)=С1+С2=1
у'(0)=2С2=1
С2=1/2; С1=1/2
у=1/2+1/2е^2х
у~=Ах^2+Вх+Д
у~'=2Ах+В
у~"=2А
у~"-2у~'=2х+1
2А-4Ах-2В=2х+1
-4А=2
2А-2В=1
Тому А=-1/2, В=-1
у=1/2+1/2е^2х-1/2х^2-х
Ответ: Y ( x ) = e²ˣ - 1/2 x² - x .
Пошаговое объяснение:
y'' - 2y' = 2x + 1 ; y( 0 ) = 1 , y'( 0 ) = 1 ;
розв"язуємо відповідне однорідне диф. рівняння : у''- 2y' = 0 . Його характеристичне рівняння k² - 2k = 0 ;
k ( k - 2 ) = 0 ; k₁ = 0 ; k₂ = 2 , тому
у = C₁ e⁰°ˣ + C₂e²ˣ = C₁ + C₂e²ˣ - це загальний розв"язок однорід. рівняння .
частинний розв"язок шукаємо у вигляді : у ₁ = х ( Ах + В ) = Ах² + Вх .
y'₁ = 2Ax + B ; y''₁ = 2A . Підставляємо у початкове рівняння :
2А - 4Ах - 2В = 2х + 1 ; звідси
{ 2A - 2B = 1 ,
{ - 4A = 2 ; A = - 1/2 ; - 1 - 2B = 1 ; 2B = - 2 ; B = - 1 ;
y ₁ = - 1/2 x² - x .
Загальний розв"язок початкового рівняння буде
Y( x ) = C₁ + C₂e²ˣ - 1/2 x² - x .
При у ( 0 ) = 1 = С₁ + С₂ * е⁰ - 1/2 * 0² - 0 ; С₁ + С₂ = 1 ;
Y'( x ) = 0 + 2C₂ * e²ˣ - x - 1 = 2C₂ * e²ˣ - x - 1 ;
Y' ( 0 ) = 2C₂* e⁰ - 0 -1 = 2C₂ - 1 = 1 ; 2C₂ = 2 ; C₂ = 1 . C₁ = 1 - 1 = 0 .
Y ( x ) = e²ˣ - 1/2 x² - x . --- це відповідь .