Предмет: Алгебра,
автор: kostchanzin092
Докажите тождество Cos^2a-sin^2a/cos^4a-sin4a
Приложения:
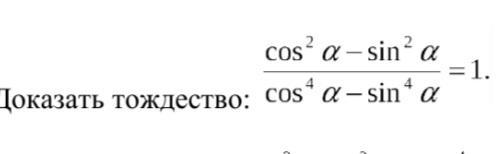
Ответы
Автор ответа:
0
Ответ:
смотрите фото
Объяснение:
... ........
Приложения:

Автор ответа:
0
Тождество доказано
Похожие вопросы
Предмет: Английский язык,
автор: Veronika20041111
Предмет: Русский язык,
автор: tagirovahadija
Предмет: Русский язык,
автор: juliaenina678
Предмет: Алгебра,
автор: onlyforalena
Предмет: Алгебра,
автор: АлискаМатвеева