Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста!!!
Приложения:
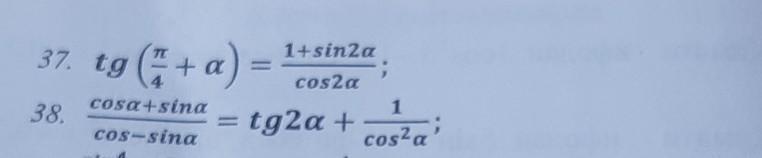
Ответы
Автор ответа:
1
Ответ:
Объяснение:
///////////////////////////////
Приложения:
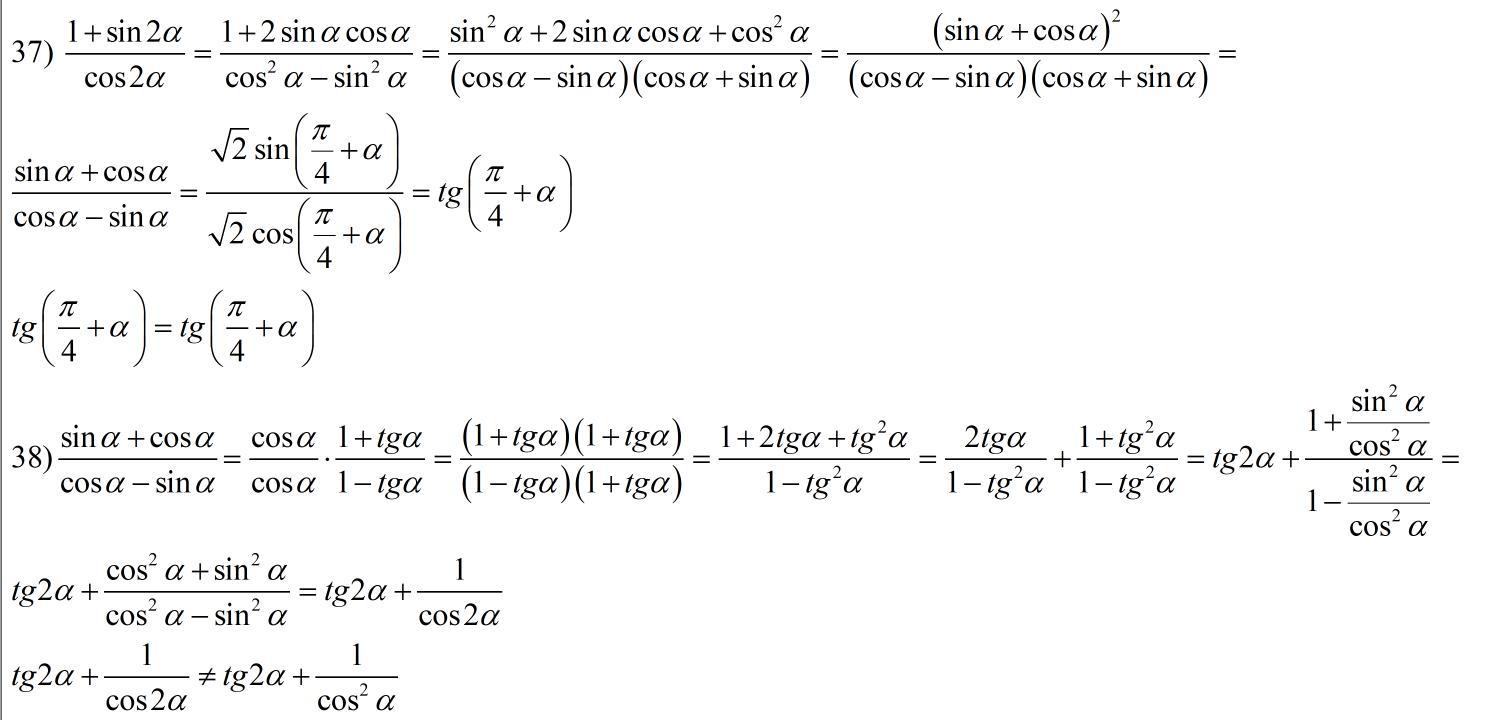
Автор ответа:
1
Ответ:
P.S. В 38 примере использовали преобразования, которые делали в 37 примере . И ещё видно, что в условии описка в правой части тождества. В знаменателе результата надо писать не квадрат косинуса, а косинус двойного угла .
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: bughlak
Предмет: Русский язык,
автор: отпоаоа
Предмет: Геометрия,
автор: Твой1демоненок
Предмет: Английский язык,
автор: Alyakaralya