Предмет: Алгебра,
автор: Аноним
Помогите решить , !!! Подробнее объясните пожалуйста!
Приложения:
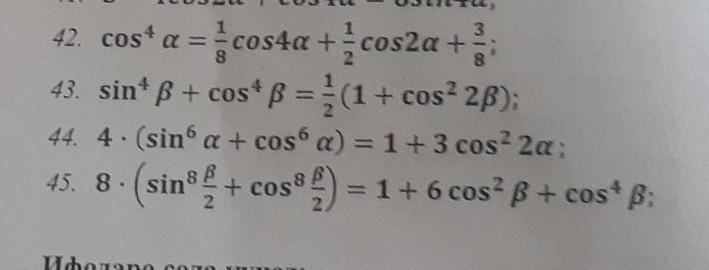
Ответы
Автор ответа:
2
P.S. Значок #43 отсылает к выкладкам в номере 43 .
Похожие вопросы
Предмет: Русский язык,
автор: egorbronnikov
Предмет: Русский язык,
автор: elina245
Предмет: Английский язык,
автор: bughlak
Предмет: История,
автор: saschinmaks201