Предмет: Алгебра,
автор: sansnope1
Решение логарифмических уравнений.
Приложения:
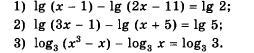
Ответы
Автор ответа:
0
1.
lg(x-1)-lg(2x-11)=lg2
Ответ:7
2.
lg(3x-1)-lg(x+5)=lg5
Ответ:-13
3.
x=0
x=±2
Ответ:2
Похожие вопросы
Предмет: Русский язык,
автор: динка20042
Предмет: Русский язык,
автор: nikita007ust
Предмет: Окружающий мир,
автор: Arisha1983
Предмет: Русский язык,
автор: qanister
Предмет: Математика,
автор: MilanaKisa232