Предмет: Алгебра,
автор: palonnaolesa
Решите систему уравнений
9x^2-xy=5; y^2-5xy=-5
Приложения:
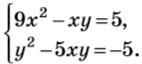
Ответы
Автор ответа:
4
Сложим уравнения:
В левой части воспользуемся формулой квадрата разности:
Выражаем у:
Подставим это соотношение, например, в первое уравнение системы:
Найдем соответствующие значения у:
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Lavrikmarina
Предмет: Українська мова,
автор: Аноним
Предмет: Українська література,
автор: BLOgER1
Предмет: Українська література,
автор: bolsovakarina