Предмет: Математика,
автор: alexanderlevochkin10
Найти общее решение дифференциальных уравнений
Приложения:
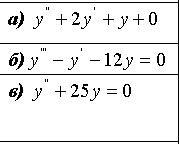
Ответы
Автор ответа:
1
Ответ:
Это однородные линейные ДУ
везде замена:
а)
б)
в)
Похожие вопросы
Предмет: Русский язык,
автор: федусь
Предмет: Русский язык,
автор: mrtchv
Предмет: Русский язык,
автор: zyxer05
Предмет: Математика,
автор: DIAMONIS
Предмет: ОБЖ,
автор: Аноним