Предмет: Математика,
автор: joil2003
Помогите пожалуйста, срочно надо
Приложения:
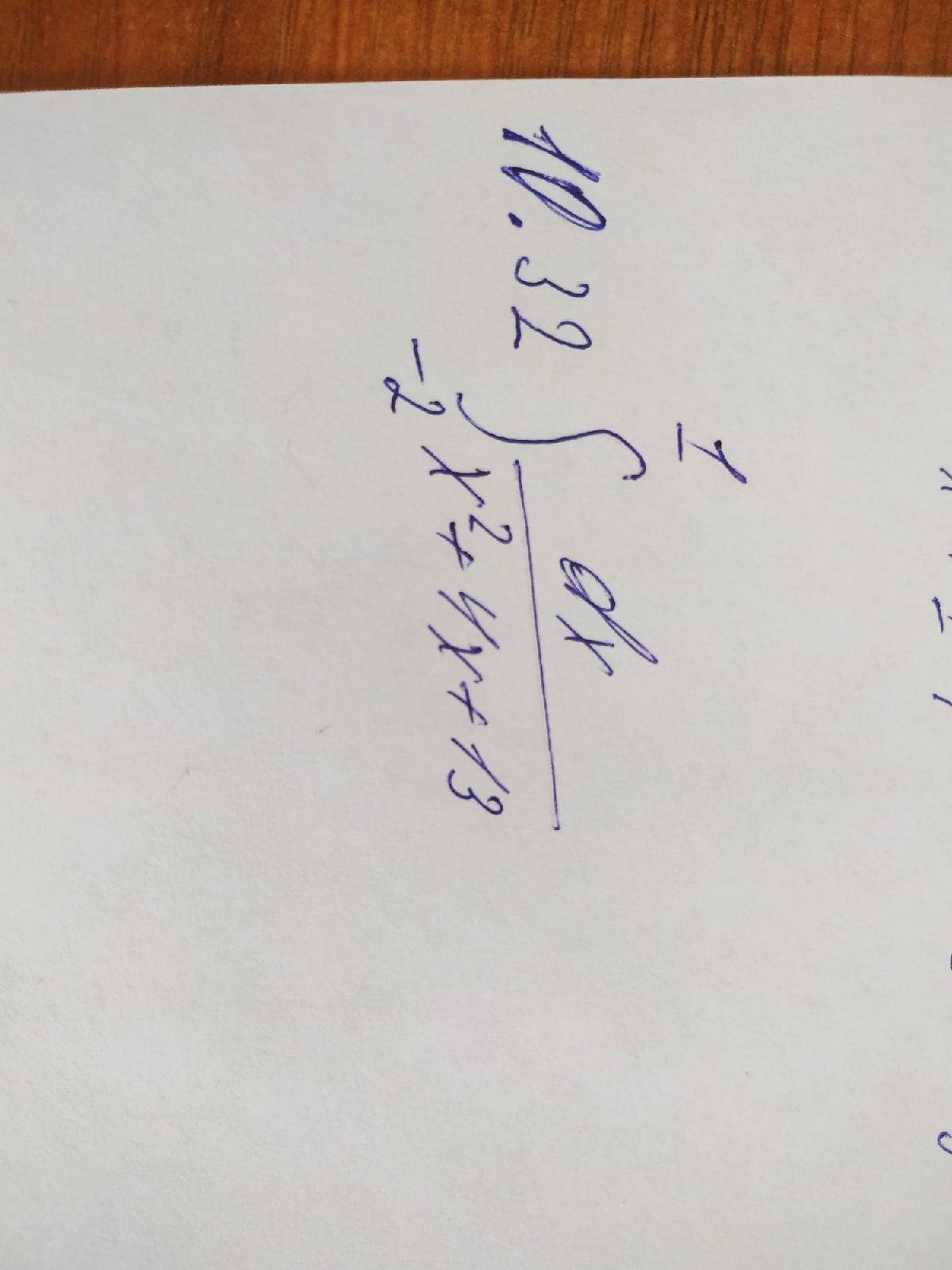
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
выделим в знаменателе полный квадрат х²+4x+13 = (x+2)²+9
дальше надо получить в знаменателе s²+1
Похожие вопросы
Предмет: Английский язык,
автор: 2006mari
Предмет: Русский язык,
автор: Katyachas
Предмет: Русский язык,
автор: nikitapos2006
Предмет: Геометрия,
автор: Radiusssimon