Question

Частица перемещается в плоскости в соответствии с уравнениями x(t) = 5t^2 + 8, y(t) = - 12t. Установить
вид траектории и определить векторы перемещения, скорости и ускорения точки через 2с после
начала движения

Answer 1

Ответ:

Объяснение:

Чтобы установить вид траектории, необходимо из уравнений исключить время:

Из второго уравнения:

t = - y / 12

Подставляем в первое:

x = 5 ·(-y/12)² + 8

x = 5·y²/144 + 8

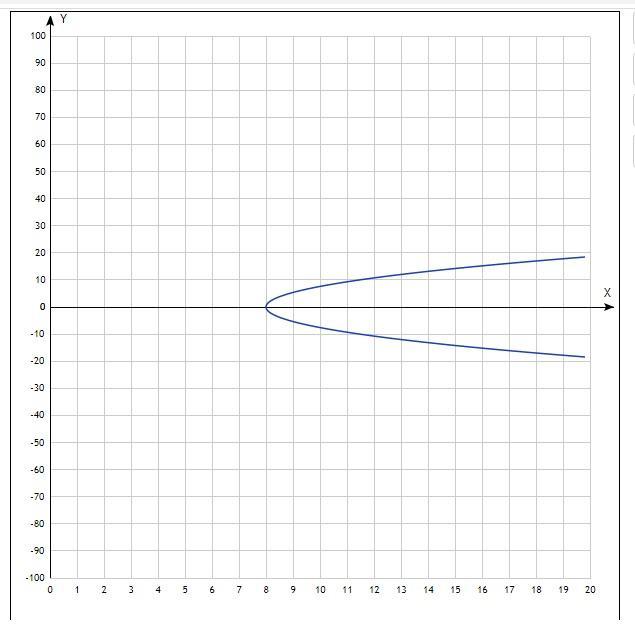
Получили уравнение параболы.

1)

Находим вектор перемещения после 2 секунд начала движения:

x(0) = 5·0² + 8 = 8  м

y(0) = - 12·0 = 0 м

x(2) = 5·2² + 8 = 28  м

y(2) = - 12·2 = -24  м

Координаты вектора перемещения:

S = { 28-8;    -24-0} = {20; -24}

Модуль вектора перемещения:

| S | = √ (20² + (-24)²) ≈ 31 м

2)

Находим вектор скорости:

vₓ(t) = x' = 10·t

vy(t) = y' = -12

vₓ(0) =  0 м/c

vy(0) = - 12 м/c

vₓ(2) = 10·2 = 20  м/c

vy(2) = - 12  м/c

V = { 20;  -12 }

| V | = √ (20² + (-12)²) ≈ 23 м/с

3)

Находим координаты вектора ускорения:

aₓ(t) = v' = 10 м/с²

ay(t) = 0

a = {10; 0}

| a | = 10 м/с²