Question

Всем ку. Может мне кто-то объяснить, почему вдруг Pin превратилось в pi + 2pn? Я так понимаю, что это одз как-то повлияло, но как именно? И кстати, почему у нас вдруг оказалось два корня под sinx = 0, ведь обычно там один Pin

Answer 1

Ответ:

а)

$\boldsymbol{x=\pi +2\pi n},\; \: n\in Z$

$\boldsymbol{x=\dfrac{\pi }{2}+2\pi m},\; \: m\in Z$

б)

$-3\pi,\; \: \; -3,5\pi$

Пошаговое объяснение:

$\dfrac{\sin x}{\sin^2\frac{x}{2}}=4\cos^2\frac{x}{2}$

ОДЗ: $\sin^2\frac{x}{2}\neq 0$

        $\dfrac{x}{2}\neq \pi n,\; \: n\in Z$    

          $x\neq 2\pi n,\; \: n\in Z$

$\sin x=4\cos^2\frac{x}{2}\cdot \sin^2\frac{x}{2}$

В правой части уравнения формула синуса двойного угла:

$4\cos^2\frac{x}{2}\cdot \sin^2\frac{x}{2}=\left(2\cos\frac{x}{2}\cdot \sin\frac{x}{2}\right)^2=\sin^2x$

$\sin x =\sin^2x$

$\sin^2x-\sin x=0$

$\sin x(\sin x-1)=0$

1) $\sin x=0$

$x=\pi n,\; \: n\in Z$

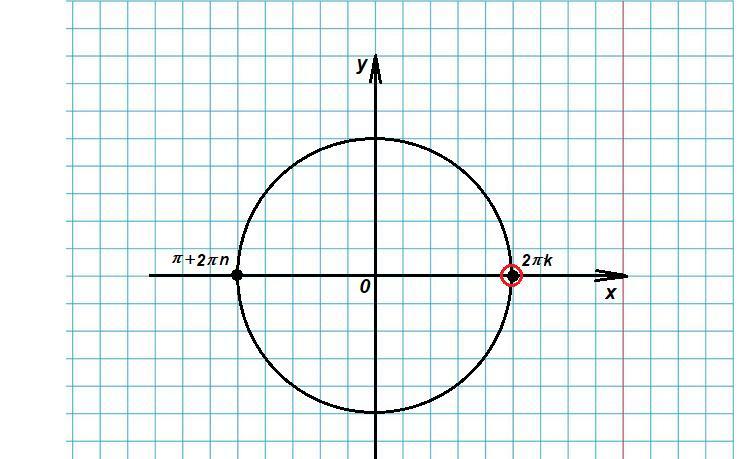
Это две точки на окружности. Но с учетом ОДЗ остается только одна точка $\boldsymbol{x=\pi +2\pi n},\; \: n\in Z.$ (см. рисунок).

2) $\sin x=1$

$\boldsymbol{x=\dfrac{\pi }{2}+2\pi m},\; \: m\in Z$

б)

$x=\pi +2\pi n$

Если $n=-2$, то $x=\pi -4\pi =\boldsymbol{-3\pi}$

$x=\dfrac{\pi}{2}+2\pi m$

Если $m=-2$, то

$x=\dfrac{\pi }{2}-4\pi=\boldsymbol{-3,5\pi}$