Предмет: Математика, автор: zarubinavaleria123

Помогите пожалуйста , даю 50 баллов ❤️❤️❤️❤️

Приложения:

kanmmu: Недостаточно условий

Travka99: Ща Батя решит

Travka99: Зачем такие ухищрения что бы найти AS когда угол D = 90 градусов SD = 13 и AD = 10

Travka99: по пифагорычу сразу находишь...

kanmmu: Travka99, здесь Пифагор не поможет, т.к. по условию не дано прямых углов кроме углов основания.

dnepr1: По рисунку видно, что грань CSD вертикальна, а SO - препендикуляр к CD и плоскости основания.

kanmmu: Извините, но когда я заканчивал школу при написании фразы "по рисунку видно" можно было указкой схлопотать... Мне по рисунку видно, что ABCD -не квадрат, а по условию квадрат. Формально в задаче не хватает условий, о чем я написал выше.

Hrisula: В учебниках встречаются задачи не только с неполными, но и, порой, абсурдными условиями. Задача дана на вполне понятном рисунке, поэтому не будем придираться. В сети много задач по нахождению площади пирамид, но конкретно такой, – чтобы уточнить условие, – не нашла. Поэтому решение дается для пирамиды с одной перпендикулярной к основанию гранью.

kanmmu: Не убедили. Выходит, задача с неполным решением по правилам сайта отмечается пользователем, затем исправляется или удаляется модератором. Но если модератор по своему усмотрению, ссылаясь на аргумент "по рисунку видно", решает задачу с допущениями, не указанными в условии, то правила на него не распространяются. Прям демократия. Вроде все равны, но кто-то равнее.

Hrisula: Решение ( РЕШЕНИЕ! ) любого задания должно быть полным и понятным. Ведь оно здесь даётся не для учителя, а для тех, кто хочет понять способ решения и в дальнейшем решать такие задачи самостоятельно. Такие ребята есть. Если есть сомнения насчет условия, то в записи решения должно быть дано уточненное условие, а нередко и его перевод . Способ решения таких задач пригодится многим пользователям. О тех, кто просто списывает, не задумываясь, не говорим. Им несть числа, как это ни грустно.

Ответы

Автор ответа: Hrisula

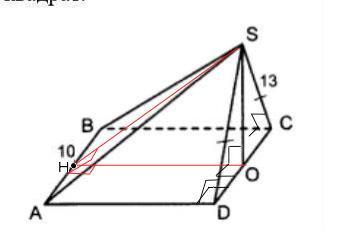
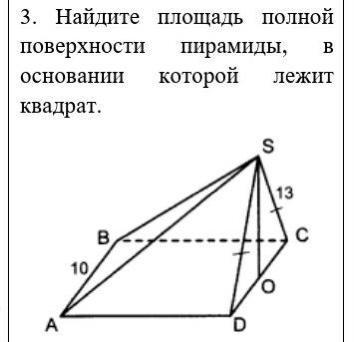
Найдите площадь полной поверхности пирамиды ЅАВСD, в основании которой лежит квадрат со стороной 10; грань DSC перпендикулярна основанию. ЅО - высота боковой грани, SD=SC=13.

Ответ: 10•(29+√61)= ≈368 (ед. площади)

Пошаговое объяснение:

Площадь полной поверхности пирамиды - сумма площадей всех её граней.

Ѕ(SABCD)=Ѕ(ABCD)+S(SCD)+2•S(SAD)+S(SAB)

Боковые грани данной пирамиды - треугольники. Два из них ( SBC и SAB) согласно т. о 3-х перпендикулярах – прямоугольные, причем они равны по катетам; а два других - равнобедренные.

1)Ѕ(ABCD)=АВ²=10²=100.

2) 2•S(SAD)=2•SD•AD:2=13•10=130

3) S(SCD)=SO•OC; ОС=DC:2=5

По т.Пифагора ЅО=12 ( вычисление сделайте сами, к тому же треугольник из Пифагоровых троек).

S(SCD)=12•5=60

4) По т. о 3-х перпендикулярах ЅН⊥АВ и является высотой ∆ ЅАВ.

S(SAB)=ЅН•АН. АН=АВ:2=5

По т.Пифагора ЅН=√(ЅО²+ОН²).

ОН||ВС=10

ЅН=√(12^2+10^2)=√244=2√61

S(SAB)=5•2√61 =10√61

5) Ѕ(SABCD)=100+130+60+10√61=10•(29+√61)= ≈368 (ед. площади)