Предмет: Математика,
автор: TanyaRamm101
Вычислить определенный интеграл
Приложения:
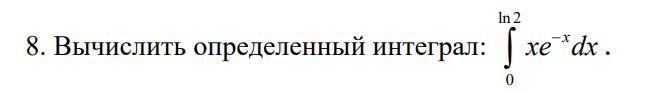
Ответы
Автор ответа:
2
Ответ:
По частям:
Похожие вопросы
Предмет: Окружающий мир,
автор: ПАТРИЧик
Предмет: Русский язык,
автор: Kanhfkzlelya
Предмет: Английский язык,
автор: mixtGn9sroA4l
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: захра20081