Предмет: Математика,
автор: sergey076
Только не просто ответ а с обьяснением!
Приложения:
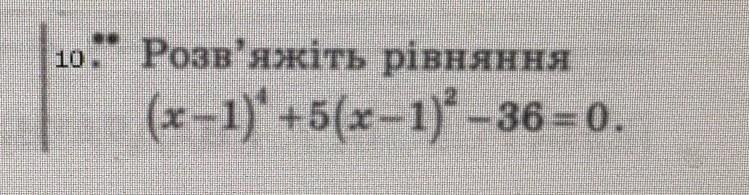
Ответы
Автор ответа:
1
Ответ:
х1 = -1 , х2 = 3
Пошаговое объяснение:
решим биквадратное уравнение. (х-1)⁴ --> представим как t² , ( х-1 )² --> представим как t
решаем дискриминант
теперь сделаем обратную подстановку : t = ( x-1 )²
здесь утверждение ложное для любого значения х, значит ответ таков :
х1 = -1 , х2 = 3
sergey076:
спасибо, добрый умный человек!)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: гульсия83
Предмет: Английский язык,
автор: ilia7894561230
Предмет: Русский язык,
автор: Котэ121234556
Предмет: Українська мова,
автор: NYatseiko