Предмет: Алгебра,
автор: oleija
Решите неравенство, пожалуйста, 15 баллов
Приложения:
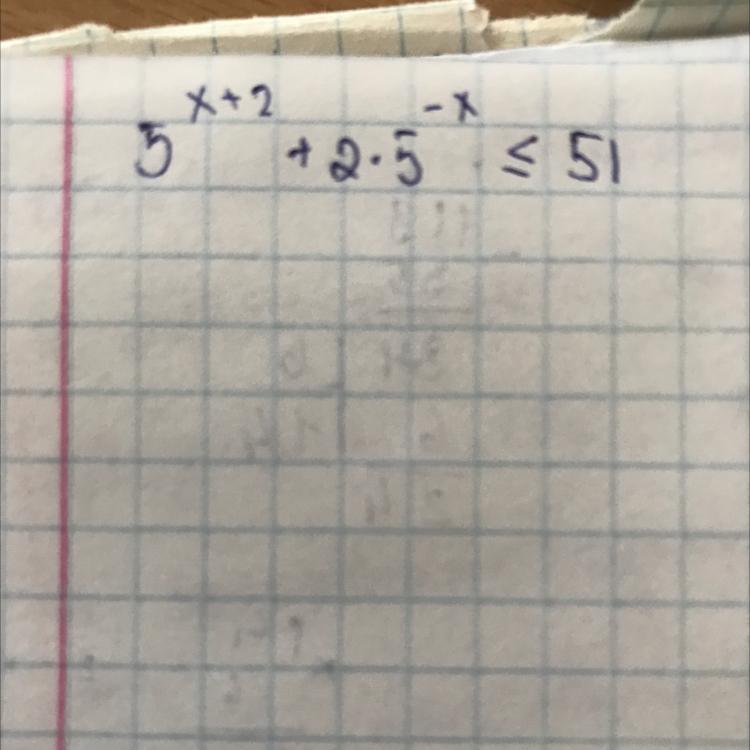
Ответы
Автор ответа:
1
Объяснение:
Пусть 5ˣ=t>0 ⇒
(5ˣ-2)*(25*5ˣ-1)≤0
-∞__+__-2__-__log₅2__+__+∞ ⇒
Ответ: x∈[-2;log₅2].
Похожие вопросы
Предмет: Русский язык,
автор: sonugold00
Предмет: Окружающий мир,
автор: savvander06
Предмет: Русский язык,
автор: анка1988
Предмет: Немецкий язык,
автор: АРЗУ20061
Предмет: Математика,
автор: NastyaWay231