Question

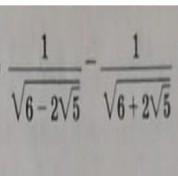
Докажите, что это число является рациональным
Можно побыстрее, пожалуйста? ​

Answer 1

Ответ:

$\dfrac{1}{\sqrt{6-2\sqrt5}}-\dfrac{1}{\sqrt{6+2\sqrt5}}=\dfrac{1}{\sqrt{(1-\sqrt5)^2}}-\dfrac{1}{\sqrt{(1+\sqrt5)^2}}=\dfrac{1}{|1-\sqrt5|}-\dfrac{1}{|1+\sqrt5|}=\\\\\\=\dfrac{1}{\sqrt5-1}-\dfrac{1}{1+\sqrt5}=\dfrac{1+\sqrt5-\sqrt5+1}{(\sqrt5-1)(\sqrt5+1)}=\dfrac{2}{5-1}=\dfrac{2}{4}=\dfrac{1}{2}$

$\dfrac{1}{2}$  - рациональное число

Answer 2

Ответ:

1/2

Объяснение:

1/√(6-2√5) -1/√(6+2√5)=1/√(1-2√5 +5) -1/√(1+2√5+5)=1/√(1-√5)² -1/√(1+√5)²=1/(√5 -1) -1/(1+√5)=(1+√5 -√5 +1))/((√5 -1)(1+√5))=2/(5-1)=2/4=1/2