Предмет: Алгебра,
автор: Maria1234566
5 заданий, 8 класс. Сделайте пожалуйста с подробным решением
Приложения:
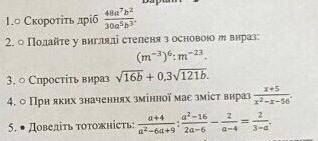
Ответы
Автор ответа:
0
№1
№2
№3
№4
ОДЗ уравнения:
Значит уравнение имеет смысл при значениях.
x∈(-∞;-7)U(-7;8)U(8;+∞)
№5
1)
2)
a-3=-(3-a)
3)
Доказано.
При делении минусы сократятся.
Похожие вопросы
Предмет: Окружающий мир,
автор: alenasestr
Предмет: Английский язык,
автор: 10Плюшевая10Ксюша10
Предмет: Русский язык,
автор: med80
Предмет: Русский язык,
автор: polina20076