Question

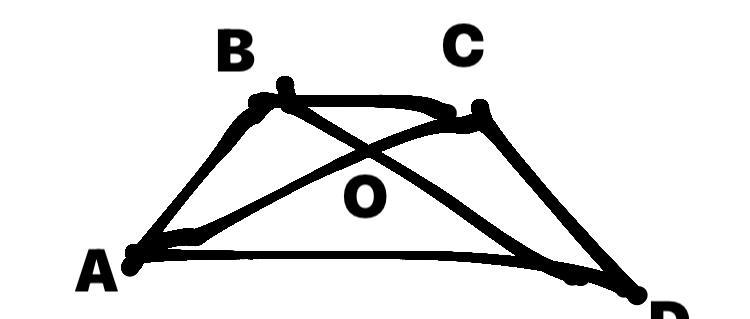
В трапеции ABCD (ВС параллельно AD) ВС = 9 см, AD = 16 см, BD = 18 см. О – точка пересечения АС и BD. Найдите CD

Answer 1

Ответ:

6,48 см

Объяснение:

АОD, BOC - подобные. (ВOC=AOD как вертикальные; уг. CBO=ADO как внутренние накрест лежащие при параллельных прямых АD и ВС и секущей ВD).

S тр-ка ВОС равна S1 = 0,5ВС·Н1

S тр-ка АОД равна S2 = 0,5АД·Н2 Н1:Н2 к -коэфиициент подобия, а S1 : S2 = к²

S1 : S2 = 0,5ВС·Н1 : 0,5АД·Н2

к² = к· ВС: АД

к = 9/16

Из подобия тех же тр-ков следует, что ОВ:ОД = 9/16, но ОД = АС - ОВ и

ОВ: (АС - ОВ) = 9/16

16·ОВ = 9·(АС - ОВ)

16·ОВ = 9·АС - 9·ОВ

25·ОВ = 9·АС

ОВ = 9·АС/25 = 9·18:25 = 6,48 (см)