Предмет: Геометрия,
автор: Matki
пожалуйста, геометрия , ничего не понимаю
Радиусы оснований усечённого конуса равны :
![r= \frac{2}{ \sqrt[4]{2} \sqrt{\pi} } и R= \frac{10}{ \sqrt[4]{2}\ \sqrt{\pi} } r= \frac{2}{ \sqrt[4]{2} \sqrt{\pi} } и R= \frac{10}{ \sqrt[4]{2}\ \sqrt{\pi} }](https://tex.z-dn.net/?f=r%3D+%5Cfrac%7B2%7D%7B+%5Csqrt%5B4%5D%7B2%7D+%5Csqrt%7B%5Cpi%7D++%7D++%D0%B8+R%3D++%5Cfrac%7B10%7D%7B+%5Csqrt%5B4%5D%7B2%7D%5C+%5Csqrt%7B%5Cpi%7D++%7D+)
а угол между его образующей и основанием равен 45∘. Найдите площадь боковой поверхности этого усечённого конуса.
Ответы
Автор ответа:
1
P.S - делать все по очереди, как указано!!!
1
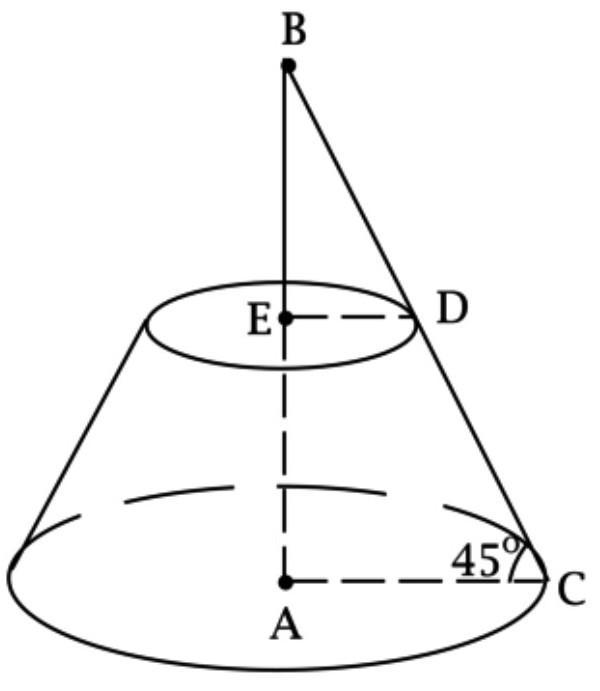
Обозначим центры оснований усечённого конуса через A и E, так что A – центр большего основания. Отметим на большем основании точку C, а точку меньшего основания, через которую проходит образующая, выходящая из C, обозначим через D.
2
Высота AE и образующая CD лежат в одной плоскости. Обозначим точку их пересечения через B. Так как AE – высота, то AE⊥CD и AE⊥AC. Рассмотрим прямоугольный треугольник BAC: в нём ∠BCA=45∘, тогда
3.(первоее фото)
4
Рассмотрим прямоугольный треугольник BED: так как ∠EBD=45∘, то
5.(первое фото)
6
тогда EA=AB−BE=R−r, DC=BC−BD=R2−r2=2(R−r). б о к Sбок=π(R+r)⋅I, где I – образующая, тогда
7(первое фото)
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Мамуля111
Предмет: Русский язык,
автор: gost7051
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: чикчик2
Предмет: Алгебра,
автор: delat