Предмет: Математика,
автор: Noname83833
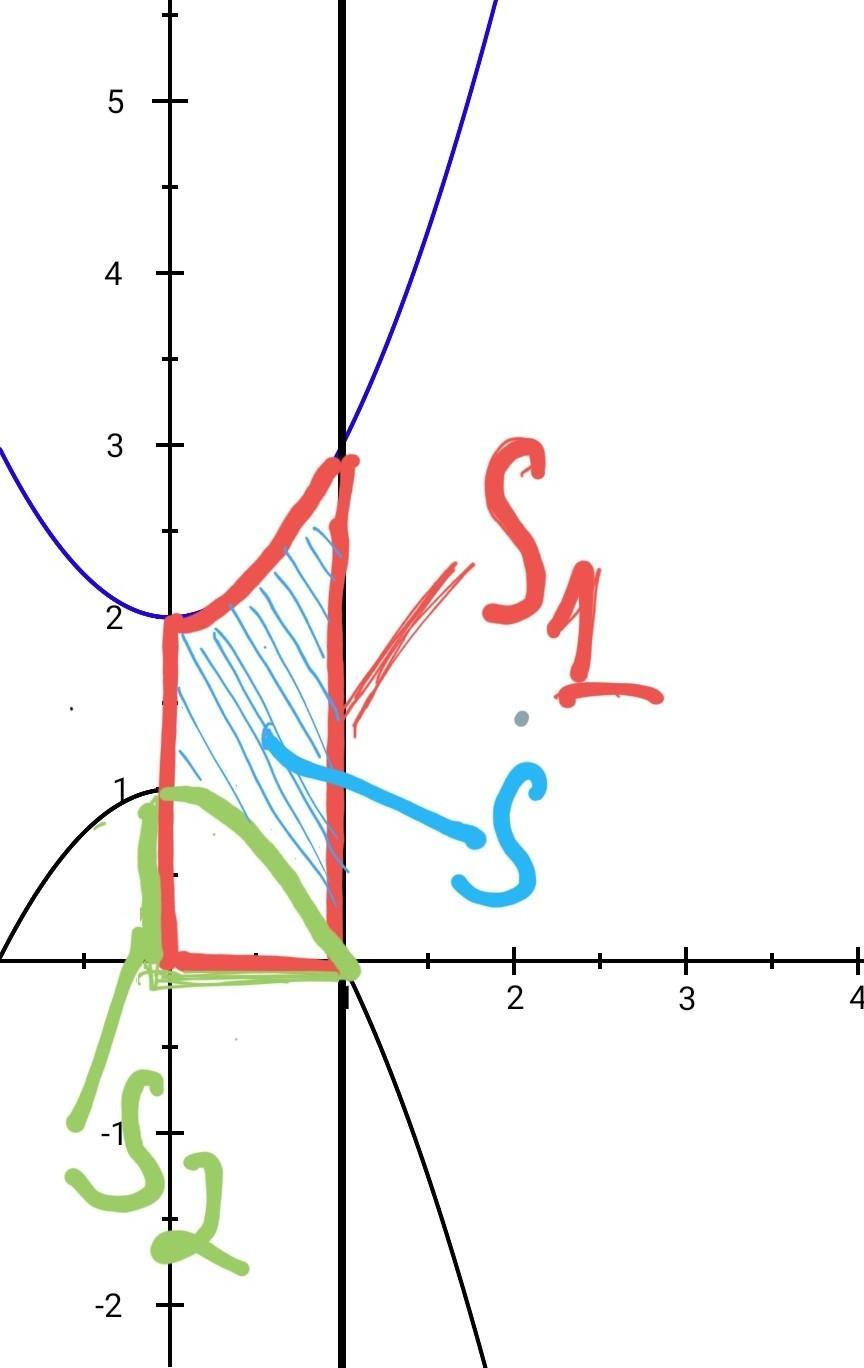
вычислить площадь фигуры ограниченой линиями y=x^2+2 ,y=1-x^2,x=0,x=1
Очень срочно ,помогите пожалуйста ,даю 15 баллов
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Приложения:
Noname83833:
Можно рисунок пожалуйста?)
приложил. Парабола ветви вверх - это у = х² + 2
Парабола ветви вниз - это у = 1 - х²
Вертикальная черта справа - это линия х = 1, а черта Оу - она же и есть линия х = 0
Похожие вопросы
Предмет: Русский язык,
автор: 14101985nata
Предмет: Русский язык,
автор: GameLove99
Предмет: Другие предметы,
автор: LenaVicu8shka
Предмет: История,
автор: dasha2247