Предмет: Алгебра,
автор: ziglerziga
Найти частную производную первого порядка.
Приложения:
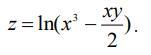
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: свирина
Предмет: Русский язык,
автор: АннаМикитенко
Предмет: Қазақ тiлi,
автор: loveyounebo
Предмет: Русский язык,
автор: Simarevaliza