Предмет: Математика,
автор: emalinkina
СРОЧНО НАДО, ДАЮ 50 БАЛЛОВ СДЕЛАТЬ ВСЕ 4 ПРИМЕРА С РЕШЕНИЕМ
Приложения:
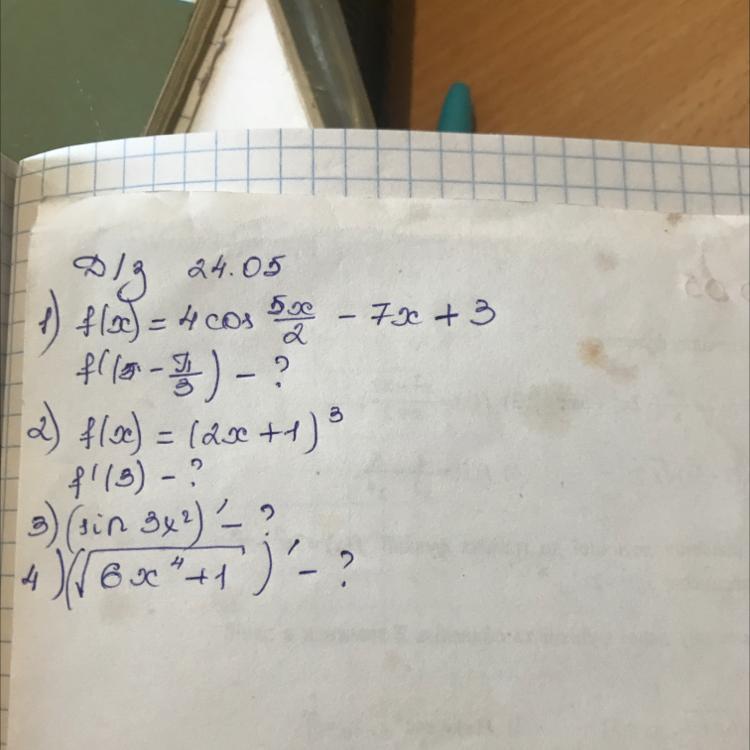
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
Похожие вопросы
Предмет: Русский язык,
автор: анна20074
Предмет: Русский язык,
автор: tornado08087
Предмет: Русский язык,
автор: Eskimoska
Предмет: История,
автор: alena0072
Предмет: Математика,
автор: DB05